ReactOS  0.4.14-dev-49-gfb4591c
Macros | Functions
clip.c File Reference
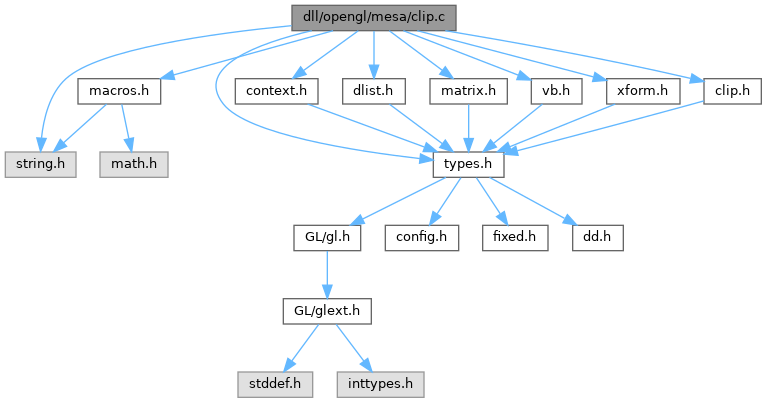
#include <string.h>
#include "clip.h"
#include "context.h"
#include "dlist.h"
#include "macros.h"
#include "matrix.h"
#include "types.h"
#include "vb.h"
#include "xform.h"
Include dependency graph for clip.c:

Go to the source code of this file.

Macros

#define LINTERP(T, A, B)   ( (A) + (T) * ( (B) - (A) ) )
 
#define EYE_SPACE   1
 
#define CLIP_SPACE   2
 
#define GENERAL_CLIP
 
#define X(I)   coord[I][0]
 
#define Y(I)   coord[I][1]
 
#define Z(I)   coord[I][2]
 
#define W(I)   coord[I][3]
 
#define OUTSIDE(K)   (X(K) > W(K))
 
#define COMPUTE_INTERSECTION(new, in, out)
 
#define OUTSIDE(K)   (X(K) < -W(K))
 
#define COMPUTE_INTERSECTION(new, in, out)
 
#define OUTSIDE(K)   (Y(K) > W(K))
 
#define COMPUTE_INTERSECTION(new, in, out)
 
#define OUTSIDE(K)   (Y(K) < -W(K))
 
#define COMPUTE_INTERSECTION(new, in, out)
 
#define OUTSIDE(K)   (Z(K) > W(K))
 
#define COMPUTE_INTERSECTION(new, in, out)
 
#define OUTSIDE(K)   (Z(K) < -W(K))
 
#define COMPUTE_INTERSECTION(new, in, out)
 
#define GENERAL_CLIP
 
#define X(I)   coord[I][0]
 
#define Y(I)   coord[I][1]
 
#define Z(I)   coord[I][2]
 
#define W(I)   coord[I][3]
 
#define INCOUNT   n
 
#define OUTCOUNT   n2
 
#define INLIST   vlist
 
#define OUTLIST   vlist2
 
#define INSIDE(K)   (X(K) <= W(K))
 
#define COMPUTE_INTERSECTION(in, out, new)
 
#define INCOUNT   n2
 
#define OUTCOUNT   n
 
#define INLIST   vlist2
 
#define OUTLIST   vlist
 
#define INSIDE(K)   (X(K) >= -W(K))
 
#define COMPUTE_INTERSECTION(in, out, new)
 
#define INCOUNT   n
 
#define OUTCOUNT   n2
 
#define INLIST   vlist
 
#define OUTLIST   vlist2
 
#define INSIDE(K)   (Y(K) <= W(K))
 
#define COMPUTE_INTERSECTION(in, out, new)
 
#define INCOUNT   n2
 
#define OUTCOUNT   n
 
#define INLIST   vlist2
 
#define OUTLIST   vlist
 
#define INSIDE(K)   (Y(K) >= -W(K))
 
#define COMPUTE_INTERSECTION(in, out, new)
 
#define INCOUNT   n
 
#define OUTCOUNT   n2
 
#define INLIST   vlist
 
#define OUTLIST   vlist2
 
#define INSIDE(K)   (Z(K) <= W(K))
 
#define COMPUTE_INTERSECTION(in, out, new)
 
#define INCOUNT   n2
 
#define OUTCOUNT   n
 
#define INLIST   vlist2
 
#define OUTLIST   vlist
 
#define INSIDE(K)   (Z(K) >= -W(K))
 
#define COMPUTE_INTERSECTION(in, out, new)
 
#define MAGIC_NUMBER   -0.8e-03F
 
#define INSIDE(J, A, B, C, D)
 
#define OUTSIDE(J, A, B, C, D)
 

Functions

void interpolate_aux (GLcontext *ctx, GLuint space, GLuint dst, GLfloat t, GLuint in, GLuint out)
 
void interpolate_aux_color_tex2 (GLcontext *ctx, GLuint space, GLuint dst, GLfloat t, GLuint in, GLuint out)
 
void interpolate_aux_tex2 (GLcontext *ctx, GLuint space, GLuint dst, GLfloat t, GLuint in, GLuint out)
 
void interpolate_aux_color (GLcontext *ctx, GLuint space, GLuint dst, GLfloat t, GLuint in, GLuint out)
 
void gl_ClipPlane (GLcontext *ctx, GLenum plane, const GLfloat *equation)
 
void gl_GetClipPlane (GLcontext *ctx, GLenum plane, GLdouble *equation)
 
GLuint gl_viewclip_point (const GLfloat v[])
 
GLuint gl_viewclip_line (GLcontext *ctx, GLuint *i, GLuint *j)
 
GLuint gl_viewclip_polygon (GLcontext *ctx, GLuint n, GLuint vlist[])
 
GLuint gl_userclip_point (GLcontext *ctx, const GLfloat v[])
 
GLuint gl_userclip_line (GLcontext *ctx, GLuint *i, GLuint *j)
 
GLuint gl_userclip_polygon (GLcontext *ctx, GLuint n, GLuint vlist[])
 

Macro Definition Documentation

◆ CLIP_SPACE

#define CLIP_SPACE   2

Definition at line 101 of file clip.c.

◆ COMPUTE_INTERSECTION [1/12]

#define COMPUTE_INTERSECTION (   new,
  in,
  out 
)
Value:
dx = X(out) - X(in); \
dw = W(out) - W(in); \
t = (X(in) - W(in)) / (dw-dx); \
X(new) = X(in) + t * dx; \
Y(new) = Y(in) + t * (Y(out) - Y(in)); \
Z(new) = Z(in) + t * (Z(out) - Z(in)); \
W(new) = W(in) + t * dw;
Y
#define Y(I)
W
#define W(I)
t
GLdouble GLdouble t
Definition: gl.h:2047
Z
#define Z(I)
out
static FILE * out
Definition: regtests2xml.c:44
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
X
#define X(I)
in
GLuint in
Definition: glext.h:9616
dx
GLint dx
Definition: linetemp.h:97

◆ COMPUTE_INTERSECTION [2/12]

#define COMPUTE_INTERSECTION (   new,
  in,
  out 
)
Value:
dx = X(out) - X(in); \
dw = W(out) - W(in); \
t = -(X(in) + W(in)) / (dw+dx); \
X(new) = X(in) + t * dx; \
Y(new) = Y(in) + t * (Y(out) - Y(in)); \
Z(new) = Z(in) + t * (Z(out) - Z(in)); \
W(new) = W(in) + t * dw;
Y
#define Y(I)
W
#define W(I)
t
GLdouble GLdouble t
Definition: gl.h:2047
Z
#define Z(I)
out
static FILE * out
Definition: regtests2xml.c:44
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
X
#define X(I)
in
GLuint in
Definition: glext.h:9616
dx
GLint dx
Definition: linetemp.h:97

◆ COMPUTE_INTERSECTION [3/12]

#define COMPUTE_INTERSECTION (   new,
  in,
  out 
)
Value:
dy = Y(out) - Y(in); \
dw = W(out) - W(in); \
t = (Y(in) - W(in)) / (dw-dy); \
X(new) = X(in) + t * (X(out) - X(in)); \
Y(new) = Y(in) + t * dy; \
Z(new) = Z(in) + t * (Z(out) - Z(in)); \
W(new) = W(in) + t * dw;
Y
#define Y(I)
dy
GLint dy
Definition: linetemp.h:97
W
#define W(I)
t
GLdouble GLdouble t
Definition: gl.h:2047
Z
#define Z(I)
out
static FILE * out
Definition: regtests2xml.c:44
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
X
#define X(I)
in
GLuint in
Definition: glext.h:9616

◆ COMPUTE_INTERSECTION [4/12]

#define COMPUTE_INTERSECTION (   new,
  in,
  out 
)
Value:
dy = Y(out) - Y(in); \
dw = W(out) - W(in); \
t = -(Y(in) + W(in)) / (dw+dy); \
X(new) = X(in) + t * (X(out) - X(in)); \
Y(new) = Y(in) + t * dy; \
Z(new) = Z(in) + t * (Z(out) - Z(in)); \
W(new) = W(in) + t * dw;
Y
#define Y(I)
dy
GLint dy
Definition: linetemp.h:97
W
#define W(I)
t
GLdouble GLdouble t
Definition: gl.h:2047
Z
#define Z(I)
out
static FILE * out
Definition: regtests2xml.c:44
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
X
#define X(I)
in
GLuint in
Definition: glext.h:9616

◆ COMPUTE_INTERSECTION [5/12]

#define COMPUTE_INTERSECTION (   new,
  in,
  out 
)
Value:
dz = Z(out) - Z(in); \
dw = W(out) - W(in); \
t = (Z(in) - W(in)) / (dw-dz); \
X(new) = X(in) + t * (X(out) - X(in)); \
Y(new) = Y(in) + t * (Y(out) - Y(in)); \
Z(new) = Z(in) + t * dz; \
W(new) = W(in) + t * dw;
Y
#define Y(I)
W
#define W(I)
t
GLdouble GLdouble t
Definition: gl.h:2047
Z
#define Z(I)
out
static FILE * out
Definition: regtests2xml.c:44
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
X
#define X(I)
in
GLuint in
Definition: glext.h:9616

◆ COMPUTE_INTERSECTION [6/12]

#define COMPUTE_INTERSECTION (   new,
  in,
  out 
)
Value:
dz = Z(out) - Z(in); \
dw = W(out) - W(in); \
t = -(Z(in) + W(in)) / (dw+dz); \
X(new) = X(in) + t * (X(out) - X(in)); \
Y(new) = Y(in) + t * (Y(out) - Y(in)); \
Z(new) = Z(in) + t * dz; \
W(new) = W(in) + t * dw;
Y
#define Y(I)
W
#define W(I)
t
GLdouble GLdouble t
Definition: gl.h:2047
Z
#define Z(I)
out
static FILE * out
Definition: regtests2xml.c:44
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
X
#define X(I)
in
GLuint in
Definition: glext.h:9616

◆ COMPUTE_INTERSECTION [7/12]

#define COMPUTE_INTERSECTION (   in,
  out,
  new 
)
Value:
dx = X(out) - X(in); \
dw = W(out) - W(in); \
t = (X(in)-W(in)) / (dw-dx); \
neww = W(in) + t * dw; \
X(new) = neww; \
Y(new) = Y(in) + t * (Y(out) - Y(in)); \
Z(new) = Z(in) + t * (Z(out) - Z(in)); \
W(new) = neww;
Y
#define Y(I)
W
#define W(I)
t
GLdouble GLdouble t
Definition: gl.h:2047
Z
#define Z(I)
out
static FILE * out
Definition: regtests2xml.c:44
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
X
#define X(I)
in
GLuint in
Definition: glext.h:9616
dx
GLint dx
Definition: linetemp.h:97

◆ COMPUTE_INTERSECTION [8/12]

#define COMPUTE_INTERSECTION (   in,
  out,
  new 
)
Value:
dx = X(out)-X(in); \
dw = W(out)-W(in); \
t = -(X(in)+W(in)) / (dw+dx); \
neww = W(in) + t * dw; \
X(new) = -neww; \
Y(new) = Y(in) + t * (Y(out) - Y(in)); \
Z(new) = Z(in) + t * (Z(out) - Z(in)); \
W(new) = neww;
Y
#define Y(I)
W
#define W(I)
t
GLdouble GLdouble t
Definition: gl.h:2047
Z
#define Z(I)
out
static FILE * out
Definition: regtests2xml.c:44
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
X
#define X(I)
in
GLuint in
Definition: glext.h:9616
dx
GLint dx
Definition: linetemp.h:97

◆ COMPUTE_INTERSECTION [9/12]

#define COMPUTE_INTERSECTION (   in,
  out,
  new 
)
Value:
dy = Y(out)-Y(in); \
dw = W(out)-W(in); \
t = (Y(in)-W(in)) / (dw-dy); \
neww = W(in) + t * dw; \
X(new) = X(in) + t * (X(out) - X(in)); \
Y(new) = neww; \
Z(new) = Z(in) + t * (Z(out) - Z(in)); \
W(new) = neww;
Y
#define Y(I)
dy
GLint dy
Definition: linetemp.h:97
W
#define W(I)
t
GLdouble GLdouble t
Definition: gl.h:2047
Z
#define Z(I)
out
static FILE * out
Definition: regtests2xml.c:44
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
X
#define X(I)
in
GLuint in
Definition: glext.h:9616

◆ COMPUTE_INTERSECTION [10/12]

#define COMPUTE_INTERSECTION (   in,
  out,
  new 
)
Value:
dy = Y(out)-Y(in); \
dw = W(out)-W(in); \
t = -(Y(in)+W(in)) / (dw+dy); \
neww = W(in) + t * dw; \
X(new) = X(in) + t * (X(out) - X(in)); \
Y(new) = -neww; \
Z(new) = Z(in) + t * (Z(out) - Z(in)); \
W(new) = neww;
Y
#define Y(I)
dy
GLint dy
Definition: linetemp.h:97
W
#define W(I)
t
GLdouble GLdouble t
Definition: gl.h:2047
Z
#define Z(I)
out
static FILE * out
Definition: regtests2xml.c:44
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
X
#define X(I)
in
GLuint in
Definition: glext.h:9616

◆ COMPUTE_INTERSECTION [11/12]

#define COMPUTE_INTERSECTION (   in,
  out,
  new 
)
Value:
dz = Z(out)-Z(in); \
dw = W(out)-W(in); \
t = (Z(in)-W(in)) / (dw-dz); \
neww = W(in) + t * dw; \
X(new) = X(in) + t * (X(out) - X(in)); \
Y(new) = Y(in) + t * (Y(out) - Y(in)); \
Z(new) = neww; \
W(new) = neww;
Y
#define Y(I)
W
#define W(I)
t
GLdouble GLdouble t
Definition: gl.h:2047
Z
#define Z(I)
out
static FILE * out
Definition: regtests2xml.c:44
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
X
#define X(I)
in
GLuint in
Definition: glext.h:9616

◆ COMPUTE_INTERSECTION [12/12]

#define COMPUTE_INTERSECTION (   in,
  out,
  new 
)
Value:
dz = Z(out)-Z(in); \
dw = W(out)-W(in); \
t = -(Z(in)+W(in)) / (dw+dz); \
neww = W(in) + t * dw; \
X(new) = X(in) + t * (X(out) - X(in)); \
Y(new) = Y(in) + t * (Y(out) - Y(in)); \
Z(new) = -neww; \
W(new) = neww;
Y
#define Y(I)
W
#define W(I)
t
GLdouble GLdouble t
Definition: gl.h:2047
Z
#define Z(I)
out
static FILE * out
Definition: regtests2xml.c:44
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
X
#define X(I)
in
GLuint in
Definition: glext.h:9616

◆ EYE_SPACE

#define EYE_SPACE   1

Definition at line 100 of file clip.c.

◆ GENERAL_CLIP [1/2]

#define GENERAL_CLIP
Value:
if (OUTSIDE(ii)) { \
if (OUTSIDE(jj)) { \
/* both verts are outside ==> return 0 */ \
return 0; \
} \
else { \
/* ii is outside, jj is inside ==> clip */ \
/* new vertex put in position VB->Free */ \
COMPUTE_INTERSECTION( VB->Free, jj, ii ) \
if (ctx->ClipMask) \
ctx->ClipInterpAuxFunc( ctx, CLIP_SPACE, VB->Free, t, jj, ii );\
ii = VB->Free; \
VB->Free++; \
if (VB->Free==VB_SIZE) VB->Free = 1; \
} \
} \
else { \
if (OUTSIDE(jj)) { \
/* ii is inside, jj is outside ==> clip */ \
/* new vertex put in position VB->Free */ \
COMPUTE_INTERSECTION( VB->Free, ii, jj ); \
if (ctx->ClipMask) \
ctx->ClipInterpAuxFunc( ctx, CLIP_SPACE, VB->Free, t, ii, jj );\
jj = VB->Free; \
VB->Free++; \
if (VB->Free==VB_SIZE) VB->Free = 1; \
} \
/* else both verts are inside ==> do nothing */ \
}
OUTSIDE
#define OUTSIDE(K)
Definition: clip.c:786
t
GLdouble GLdouble t
Definition: gl.h:2047
VB
struct vertex_buffer * VB
Definition: tritemp.h:139
VB_SIZE
#define VB_SIZE
Definition: vb.h:89
CLIP_SPACE
#define CLIP_SPACE
Definition: clip.c:101

◆ GENERAL_CLIP [2/2]

#define GENERAL_CLIP

◆ INCOUNT [1/6]

#define INCOUNT   n

◆ INCOUNT [2/6]

#define INCOUNT   n2

◆ INCOUNT [3/6]

#define INCOUNT   n

◆ INCOUNT [4/6]

#define INCOUNT   n2

◆ INCOUNT [5/6]

#define INCOUNT   n

◆ INCOUNT [6/6]

#define INCOUNT   n2

◆ INLIST [1/6]

#define INLIST   vlist

◆ INLIST [2/6]

#define INLIST   vlist2

◆ INLIST [3/6]

#define INLIST   vlist

◆ INLIST [4/6]

#define INLIST   vlist2

◆ INLIST [5/6]

#define INLIST   vlist

◆ INLIST [6/6]

#define INLIST   vlist2

◆ INSIDE [1/7]

#define INSIDE (   K)    (X(K) <= W(K))

Definition at line 780 of file clip.c.

◆ INSIDE [2/7]

#define INSIDE (   K)    (X(K) >= -W(K))

Definition at line 780 of file clip.c.

◆ INSIDE [3/7]

#define INSIDE (   K)    (Y(K) <= W(K))

Definition at line 780 of file clip.c.

◆ INSIDE [4/7]

#define INSIDE (   K)    (Y(K) >= -W(K))

Definition at line 780 of file clip.c.

◆ INSIDE [5/7]

#define INSIDE (   K)    (Z(K) <= W(K))

Definition at line 780 of file clip.c.

◆ INSIDE [6/7]

#define INSIDE (   K)    (Z(K) >= -W(K))

Definition at line 780 of file clip.c.

◆ INSIDE [7/7]

#define INSIDE (   J,
  A,
  B,
  C,
  D 
)
Value:
( (VB->Eye[J][0] * A + VB->Eye[J][1] * B \
+ VB->Eye[J][2] * C + VB->Eye[J][3] * D) >= MAGIC_NUMBER )
MAGIC_NUMBER
#define MAGIC_NUMBER
Definition: clip.c:776
A
Definition: ttei1.cpp:12
VB
struct vertex_buffer * VB
Definition: tritemp.h:139
D
#define D(name, bit)
C
Definition: ttei6.cpp:27
B
#define B(row, col)

Definition at line 780 of file clip.c.

◆ LINTERP

#define LINTERP (   T,
  A,
  B 
)    ( (A) + (T) * ( (B) - (A) ) )

Definition at line 96 of file clip.c.

◆ MAGIC_NUMBER

#define MAGIC_NUMBER   -0.8e-03F

Definition at line 776 of file clip.c.

◆ OUTCOUNT [1/6]

#define OUTCOUNT   n2

◆ OUTCOUNT [2/6]

#define OUTCOUNT   n

◆ OUTCOUNT [3/6]

#define OUTCOUNT   n2

◆ OUTCOUNT [4/6]

#define OUTCOUNT   n

◆ OUTCOUNT [5/6]

#define OUTCOUNT   n2

◆ OUTCOUNT [6/6]

#define OUTCOUNT   n

◆ OUTLIST [1/6]

#define OUTLIST   vlist2

◆ OUTLIST [2/6]

#define OUTLIST   vlist

◆ OUTLIST [3/6]

#define OUTLIST   vlist2

◆ OUTLIST [4/6]

#define OUTLIST   vlist

◆ OUTLIST [5/6]

#define OUTLIST   vlist2

◆ OUTLIST [6/6]

#define OUTLIST   vlist

◆ OUTSIDE [1/7]

#define OUTSIDE (   K)    (X(K) > W(K))

Definition at line 786 of file clip.c.

◆ OUTSIDE [2/7]

#define OUTSIDE (   K)    (X(K) < -W(K))

Definition at line 786 of file clip.c.

◆ OUTSIDE [3/7]

#define OUTSIDE (   K)    (Y(K) > W(K))

Definition at line 786 of file clip.c.

◆ OUTSIDE [4/7]

#define OUTSIDE (   K)    (Y(K) < -W(K))

Definition at line 786 of file clip.c.

◆ OUTSIDE [5/7]

#define OUTSIDE (   K)    (Z(K) > W(K))

Definition at line 786 of file clip.c.

◆ OUTSIDE [6/7]

#define OUTSIDE (   K)    (Z(K) < -W(K))

Definition at line 786 of file clip.c.

◆ OUTSIDE [7/7]

#define OUTSIDE (   J,
  A,
  B,
  C,
  D 
)
Value:
( (VB->Eye[J][0] * A + VB->Eye[J][1] * B \
+ VB->Eye[J][2] * C + VB->Eye[J][3] * D) < MAGIC_NUMBER )
MAGIC_NUMBER
#define MAGIC_NUMBER
Definition: clip.c:776
A
Definition: ttei1.cpp:12
VB
struct vertex_buffer * VB
Definition: tritemp.h:139
D
#define D(name, bit)
C
Definition: ttei6.cpp:27
B
#define B(row, col)

Definition at line 786 of file clip.c.

◆ W [1/2]

#define W (   I)    coord[I][3]

◆ W [2/2]

#define W (   I)    coord[I][3]

◆ X [1/2]

#define X (   I)    coord[I][0]

◆ X [2/2]

#define X (   I)    coord[I][0]

◆ Y [1/2]

#define Y (   I)    coord[I][1]

◆ Y [2/2]

#define Y (   I)    coord[I][1]

◆ Z [1/2]

#define Z (   I)    coord[I][2]

◆ Z [2/2]

#define Z (   I)    coord[I][2]

Function Documentation

◆ gl_ClipPlane()

void gl_ClipPlane ( GLcontext *  ctx,
GLenum  plane,
const GLfloat *  equation 
)

Definition at line 204 of file clip.c.

205 {
206  GLint p;
207 
208  p = (GLint) plane - (GLint) GL_CLIP_PLANE0;
209  if (p<0 || p>=MAX_CLIP_PLANES) {
210  gl_error( ctx, GL_INVALID_ENUM, "glClipPlane" );
211  return;
212  }
213 
214  /*
215  * The equation is transformed by the transpose of the inverse of the
216  * current modelview matrix and stored in the resulting eye coordinates.
217  */
218  if (ctx->NewModelViewMatrix) {
219  gl_analyze_modelview_matrix(ctx);
220  }
221  gl_transform_vector( ctx->Transform.ClipEquation[p], equation,
222  ctx->ModelViewInv );
223 }
plane
GLsizei GLenum const GLvoid GLsizei GLenum GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLint GLint GLint GLshort GLshort GLshort GLubyte GLubyte GLubyte GLuint GLuint GLuint GLushort GLushort GLushort GLbyte GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLfloat GLint GLint GLint GLint GLshort GLshort GLshort GLshort GLubyte GLubyte GLubyte GLubyte GLuint GLuint GLuint GLuint GLushort GLushort GLushort GLushort GLboolean const GLdouble const GLfloat const GLint const GLshort const GLbyte const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLdouble const GLfloat const GLfloat const GLint const GLint const GLshort const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort GLenum GLenum GLenum GLfloat GLenum GLint GLenum GLenum GLenum GLfloat GLenum GLenum GLint GLenum GLfloat GLenum GLint GLint GLushort GLenum GLenum GLfloat GLenum GLenum GLint GLfloat const GLubyte GLenum GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLint GLint GLsizei GLsizei GLint GLenum GLenum const GLvoid GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLenum const GLdouble GLenum GLenum const GLfloat GLenum GLenum const GLint GLsizei GLuint GLfloat GLuint GLbitfield GLfloat GLint GLuint GLboolean GLenum GLfloat GLenum GLbitfield GLenum GLfloat GLfloat GLint GLint const GLfloat GLenum GLfloat GLfloat GLint GLint GLfloat GLfloat GLint GLint const GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat const GLdouble const GLfloat const GLdouble const GLfloat GLint GLint GLint GLenum GLenum GLenum GLint GLuint GLenum GLenum GLfloat GLenum GLfloat GLenum GLint const GLfloat GLenum GLint const GLushort GLint GLint GLsizei GLsizei GLenum GLsizei GLsizei GLenum GLenum const GLvoid GLenum plane
Definition: glfuncs.h:270
gl_context::NewModelViewMatrix
GLboolean NewModelViewMatrix
Definition: types.h:1282
gl_transform_vector
void gl_transform_vector(GLfloat u[4], const GLfloat v[4], const GLfloat m[16])
Definition: xform.c:248
MAX_CLIP_PLANES
#define MAX_CLIP_PLANES
Definition: config.h:87
gl_context::ModelViewInv
GLfloat ModelViewInv[16]
Definition: types.h:1285
GL_CLIP_PLANE0
#define GL_CLIP_PLANE0
Definition: gl.h:346
gl_context::Transform
struct gl_transform_attrib Transform
Definition: types.h:1335
gl_error
void gl_error(GLcontext *ctx, GLenum error, const char *s)
Definition: context.c:1421
equation
GLsizei GLenum const GLvoid GLsizei GLenum GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLint GLint GLint GLshort GLshort GLshort GLubyte GLubyte GLubyte GLuint GLuint GLuint GLushort GLushort GLushort GLbyte GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLfloat GLint GLint GLint GLint GLshort GLshort GLshort GLshort GLubyte GLubyte GLubyte GLubyte GLuint GLuint GLuint GLuint GLushort GLushort GLushort GLushort GLboolean const GLdouble const GLfloat const GLint const GLshort const GLbyte const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLdouble const GLfloat const GLfloat const GLint const GLint const GLshort const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort GLenum GLenum GLenum GLfloat GLenum GLint GLenum GLenum GLenum GLfloat GLenum GLenum GLint GLenum GLfloat GLenum GLint GLint GLushort GLenum GLenum GLfloat GLenum GLenum GLint GLfloat const GLubyte GLenum GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLint GLint GLsizei GLsizei GLint GLenum GLenum const GLvoid GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLenum const GLdouble GLenum GLenum const GLfloat GLenum GLenum const GLint GLsizei GLuint GLfloat GLuint GLbitfield GLfloat GLint GLuint GLboolean GLenum GLfloat GLenum GLbitfield GLenum GLfloat GLfloat GLint GLint const GLfloat GLenum GLfloat GLfloat GLint GLint GLfloat GLfloat GLint GLint const GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat const GLdouble const GLfloat const GLdouble const GLfloat GLint GLint GLint GLenum GLenum GLenum GLint GLuint GLenum GLenum GLfloat GLenum GLfloat GLenum GLint const GLfloat GLenum GLint const GLushort GLint GLint GLsizei GLsizei GLenum GLsizei GLsizei GLenum GLenum const GLvoid GLenum GLdouble * equation
Definition: glfuncs.h:270
GL_INVALID_ENUM
#define GL_INVALID_ENUM
Definition: gl.h:694
gl_analyze_modelview_matrix
void gl_analyze_modelview_matrix(GLcontext *ctx)
Definition: matrix.c:420
GLint
int GLint
Definition: gl.h:156
p
GLfloat GLfloat p
Definition: glext.h:8902

Referenced by execute_list(), and init_exec_pointers().

◆ gl_GetClipPlane()

void gl_GetClipPlane ( GLcontext *  ctx,
GLenum  plane,
GLdouble *  equation 
)

Definition at line 227 of file clip.c.

228 {
229  GLint p;
230 
231  if (INSIDE_BEGIN_END(ctx)) {
232  gl_error( ctx, GL_INVALID_OPERATION, "glGetClipPlane" );
233  return;
234  }
235 
236  p = (GLint) (plane - GL_CLIP_PLANE0);
237  if (p<0 || p>=MAX_CLIP_PLANES) {
238  gl_error( ctx, GL_INVALID_ENUM, "glGetClipPlane" );
239  return;
240  }
241 
242  equation[0] = (GLdouble) ctx->Transform.ClipEquation[p][0];
243  equation[1] = (GLdouble) ctx->Transform.ClipEquation[p][1];
244  equation[2] = (GLdouble) ctx->Transform.ClipEquation[p][2];
245  equation[3] = (GLdouble) ctx->Transform.ClipEquation[p][3];
246 }
GLdouble
double GLdouble
Definition: gl.h:163
plane
GLsizei GLenum const GLvoid GLsizei GLenum GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLint GLint GLint GLshort GLshort GLshort GLubyte GLubyte GLubyte GLuint GLuint GLuint GLushort GLushort GLushort GLbyte GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLfloat GLint GLint GLint GLint GLshort GLshort GLshort GLshort GLubyte GLubyte GLubyte GLubyte GLuint GLuint GLuint GLuint GLushort GLushort GLushort GLushort GLboolean const GLdouble const GLfloat const GLint const GLshort const GLbyte const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLdouble const GLfloat const GLfloat const GLint const GLint const GLshort const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort GLenum GLenum GLenum GLfloat GLenum GLint GLenum GLenum GLenum GLfloat GLenum GLenum GLint GLenum GLfloat GLenum GLint GLint GLushort GLenum GLenum GLfloat GLenum GLenum GLint GLfloat const GLubyte GLenum GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLint GLint GLsizei GLsizei GLint GLenum GLenum const GLvoid GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLenum const GLdouble GLenum GLenum const GLfloat GLenum GLenum const GLint GLsizei GLuint GLfloat GLuint GLbitfield GLfloat GLint GLuint GLboolean GLenum GLfloat GLenum GLbitfield GLenum GLfloat GLfloat GLint GLint const GLfloat GLenum GLfloat GLfloat GLint GLint GLfloat GLfloat GLint GLint const GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat const GLdouble const GLfloat const GLdouble const GLfloat GLint GLint GLint GLenum GLenum GLenum GLint GLuint GLenum GLenum GLfloat GLenum GLfloat GLenum GLint const GLfloat GLenum GLint const GLushort GLint GLint GLsizei GLsizei GLenum GLsizei GLsizei GLenum GLenum const GLvoid GLenum plane
Definition: glfuncs.h:270
INSIDE_BEGIN_END
#define INSIDE_BEGIN_END(CTX)
Definition: macros.h:135
MAX_CLIP_PLANES
#define MAX_CLIP_PLANES
Definition: config.h:87
GL_CLIP_PLANE0
#define GL_CLIP_PLANE0
Definition: gl.h:346
gl_context::Transform
struct gl_transform_attrib Transform
Definition: types.h:1335
GL_INVALID_OPERATION
#define GL_INVALID_OPERATION
Definition: gl.h:696
gl_error
void gl_error(GLcontext *ctx, GLenum error, const char *s)
Definition: context.c:1421
equation
GLsizei GLenum const GLvoid GLsizei GLenum GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLint GLint GLint GLshort GLshort GLshort GLubyte GLubyte GLubyte GLuint GLuint GLuint GLushort GLushort GLushort GLbyte GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLfloat GLint GLint GLint GLint GLshort GLshort GLshort GLshort GLubyte GLubyte GLubyte GLubyte GLuint GLuint GLuint GLuint GLushort GLushort GLushort GLushort GLboolean const GLdouble const GLfloat const GLint const GLshort const GLbyte const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLdouble const GLfloat const GLfloat const GLint const GLint const GLshort const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort GLenum GLenum GLenum GLfloat GLenum GLint GLenum GLenum GLenum GLfloat GLenum GLenum GLint GLenum GLfloat GLenum GLint GLint GLushort GLenum GLenum GLfloat GLenum GLenum GLint GLfloat const GLubyte GLenum GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLint GLint GLsizei GLsizei GLint GLenum GLenum const GLvoid GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLenum const GLdouble GLenum GLenum const GLfloat GLenum GLenum const GLint GLsizei GLuint GLfloat GLuint GLbitfield GLfloat GLint GLuint GLboolean GLenum GLfloat GLenum GLbitfield GLenum GLfloat GLfloat GLint GLint const GLfloat GLenum GLfloat GLfloat GLint GLint GLfloat GLfloat GLint GLint const GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat const GLdouble const GLfloat const GLdouble const GLfloat GLint GLint GLint GLenum GLenum GLenum GLint GLuint GLenum GLenum GLfloat GLenum GLfloat GLenum GLint const GLfloat GLenum GLint const GLushort GLint GLint GLsizei GLsizei GLenum GLsizei GLsizei GLenum GLenum const GLvoid GLenum GLdouble * equation
Definition: glfuncs.h:270
GL_INVALID_ENUM
#define GL_INVALID_ENUM
Definition: gl.h:694
GLint
int GLint
Definition: gl.h:156
p
GLfloat GLfloat p
Definition: glext.h:8902

Referenced by init_dlist_pointers(), and init_exec_pointers().

◆ gl_userclip_line()

GLuint gl_userclip_line ( GLcontext *  ctx,
GLuint *  i,
GLuint *  j 
)

Definition at line 798 of file clip.c.

799 {
800  struct vertex_buffer* VB = ctx->VB;
801 
802  GLuint p, ii, jj;
803 
804  ii = *i;
805  jj = *j;
806 
807  for (p=0;p<MAX_CLIP_PLANES;p++) {
808  if (ctx->Transform.ClipEnabled[p]) {
809  register GLfloat a, b, c, d;
810  a = ctx->Transform.ClipEquation[p][0];
811  b = ctx->Transform.ClipEquation[p][1];
812  c = ctx->Transform.ClipEquation[p][2];
813  d = ctx->Transform.ClipEquation[p][3];
814 
815  if (OUTSIDE( ii, a,b,c,d )) {
816  if (OUTSIDE( jj, a,b,c,d )) {
817  /* ii and jj outside ==> quit */
818  return 0;
819  }
820  else {
821  /* ii is outside, jj is inside ==> clip */
822  GLfloat dx, dy, dz, dw, t, denom;
823  dx = VB->Eye[ii][0] - VB->Eye[jj][0];
824  dy = VB->Eye[ii][1] - VB->Eye[jj][1];
825  dz = VB->Eye[ii][2] - VB->Eye[jj][2];
826  dw = VB->Eye[ii][3] - VB->Eye[jj][3];
827  denom = dx*a + dy*b + dz*c + dw*d;
828  if (denom==0.0) {
829  t = 0.0;
830  }
831  else {
832  t = -(VB->Eye[jj][0]*a+VB->Eye[jj][1]*b
833  +VB->Eye[jj][2]*c+VB->Eye[jj][3]*d) / denom;
834  if (t>1.0F) t = 1.0F;
835  }
836  VB->Eye[VB->Free][0] = VB->Eye[jj][0] + t * dx;
837  VB->Eye[VB->Free][1] = VB->Eye[jj][1] + t * dy;
838  VB->Eye[VB->Free][2] = VB->Eye[jj][2] + t * dz;
839  VB->Eye[VB->Free][3] = VB->Eye[jj][3] + t * dw;
840 
841  /* Interpolate colors, indexes, and/or texture coords */
842  if (ctx->ClipMask)
843  interpolate_aux( ctx, EYE_SPACE, VB->Free, t, jj, ii );
844 
845  ii = VB->Free;
846  VB->Free++;
847  if (VB->Free==VB_SIZE) VB->Free = 1;
848  }
849  }
850  else {
851  if (OUTSIDE( jj, a,b,c,d )) {
852  /* ii is inside, jj is outside ==> clip */
853  GLfloat dx, dy, dz, dw, t, denom;
854  dx = VB->Eye[jj][0] - VB->Eye[ii][0];
855  dy = VB->Eye[jj][1] - VB->Eye[ii][1];
856  dz = VB->Eye[jj][2] - VB->Eye[ii][2];
857  dw = VB->Eye[jj][3] - VB->Eye[ii][3];
858  denom = dx*a + dy*b + dz*c + dw*d;
859  if (denom==0.0) {
860  t = 0.0;
861  }
862  else {
863  t = -(VB->Eye[ii][0]*a+VB->Eye[ii][1]*b
864  +VB->Eye[ii][2]*c+VB->Eye[ii][3]*d) / denom;
865  if (t>1.0F) t = 1.0F;
866  }
867  VB->Eye[VB->Free][0] = VB->Eye[ii][0] + t * dx;
868  VB->Eye[VB->Free][1] = VB->Eye[ii][1] + t * dy;
869  VB->Eye[VB->Free][2] = VB->Eye[ii][2] + t * dz;
870  VB->Eye[VB->Free][3] = VB->Eye[ii][3] + t * dw;
871 
872  /* Interpolate colors, indexes, and/or texture coords */
873  if (ctx->ClipMask)
874  interpolate_aux( ctx, EYE_SPACE, VB->Free, t, ii, jj );
875 
876  jj = VB->Free;
877  VB->Free++;
878  if (VB->Free==VB_SIZE) VB->Free = 1;
879  }
880  else {
881  /* ii and jj inside ==> do nothing */
882  }
883  }
884  }
885  }
886 
887  *i = ii;
888  *j = jj;
889  return 1;
890 }
OUTSIDE
#define OUTSIDE(K)
Definition: clip.c:786
EYE_SPACE
#define EYE_SPACE
Definition: clip.c:100
dy
GLint dy
Definition: linetemp.h:97
t
GLdouble GLdouble t
Definition: gl.h:2047
gl_context::ClipMask
GLuint ClipMask
Definition: types.h:1359
i
GLsizei GLenum const GLvoid GLsizei GLenum GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLint GLint GLint GLshort GLshort GLshort GLubyte GLubyte GLubyte GLuint GLuint GLuint GLushort GLushort GLushort GLbyte GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLfloat GLint GLint GLint GLint GLshort GLshort GLshort GLshort GLubyte GLubyte GLubyte GLubyte GLuint GLuint GLuint GLuint GLushort GLushort GLushort GLushort GLboolean const GLdouble const GLfloat const GLint const GLshort const GLbyte const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLdouble const GLfloat const GLfloat const GLint const GLint const GLshort const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort GLenum GLenum GLenum GLfloat GLenum GLint GLenum GLenum GLenum GLfloat GLenum GLenum GLint GLenum GLfloat GLenum GLint GLint GLushort GLenum GLenum GLfloat GLenum GLenum GLint GLfloat const GLubyte GLenum GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLint GLint GLsizei GLsizei GLint GLenum GLenum const GLvoid GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLenum const GLdouble GLenum GLenum const GLfloat GLenum GLenum const GLint GLsizei GLuint GLfloat GLuint GLbitfield GLfloat GLint GLuint GLboolean GLenum GLfloat GLenum GLbitfield GLenum GLfloat GLfloat GLint GLint const GLfloat GLenum GLfloat GLfloat GLint GLint GLfloat GLfloat GLint GLint const GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat const GLdouble const GLfloat const GLdouble const GLfloat GLint i
Definition: glfuncs.h:248
a
#define a
Definition: ke_i.h:78
interpolate_aux
void interpolate_aux(GLcontext *ctx, GLuint space, GLuint dst, GLfloat t, GLuint in, GLuint out)
Definition: clip.c:116
b
#define b
Definition: ke_i.h:79
j
GLsizei GLenum const GLvoid GLsizei GLenum GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLint GLint GLint GLshort GLshort GLshort GLubyte GLubyte GLubyte GLuint GLuint GLuint GLushort GLushort GLushort GLbyte GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLfloat GLint GLint GLint GLint GLshort GLshort GLshort GLshort GLubyte GLubyte GLubyte GLubyte GLuint GLuint GLuint GLuint GLushort GLushort GLushort GLushort GLboolean const GLdouble const GLfloat const GLint const GLshort const GLbyte const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLdouble const GLfloat const GLfloat const GLint const GLint const GLshort const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort GLenum GLenum GLenum GLfloat GLenum GLint GLenum GLenum GLenum GLfloat GLenum GLenum GLint GLenum GLfloat GLenum GLint GLint GLushort GLenum GLenum GLfloat GLenum GLenum GLint GLfloat const GLubyte GLenum GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLint GLint GLsizei GLsizei GLint GLenum GLenum const GLvoid GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLenum const GLdouble GLenum GLenum const GLfloat GLenum GLenum const GLint GLsizei GLuint GLfloat GLuint GLbitfield GLfloat GLint GLuint GLboolean GLenum GLfloat GLenum GLbitfield GLenum GLfloat GLfloat GLint GLint const GLfloat GLenum GLfloat GLfloat GLint GLint GLfloat GLfloat GLint GLint const GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat const GLdouble const GLfloat const GLdouble const GLfloat GLint GLint GLint j
Definition: glfuncs.h:250
b
GLboolean GLboolean GLboolean b
Definition: glext.h:6204
MAX_CLIP_PLANES
#define MAX_CLIP_PLANES
Definition: config.h:87
d
#define d
Definition: ke_i.h:81
c
const GLubyte * c
Definition: glext.h:8905
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
gl_context::Transform
struct gl_transform_attrib Transform
Definition: types.h:1335
vertex_buffer
Definition: vb.h:99
VB
struct vertex_buffer * VB
Definition: tritemp.h:139
VB_SIZE
#define VB_SIZE
Definition: vb.h:89
GLuint
unsigned int GLuint
Definition: gl.h:159
dx
GLint dx
Definition: linetemp.h:97
GLfloat
float GLfloat
Definition: gl.h:161
c
#define c
Definition: ke_i.h:80
a
GLboolean GLboolean GLboolean GLboolean a
Definition: glext.h:6204
p
GLfloat GLfloat p
Definition: glext.h:8902
gl_context::VB
struct vertex_buffer * VB
Definition: types.h:1380
F
#define F(x, y, z)
Definition: md5.c:51

Referenced by render_clipped_line().

◆ gl_userclip_point()

GLuint gl_userclip_point ( GLcontext *  ctx,
const GLfloat  v[] 
)

Definition at line 756 of file clip.c.

757 {
758  GLuint p;
759 
760  for (p=0;p<MAX_CLIP_PLANES;p++) {
761  if (ctx->Transform.ClipEnabled[p]) {
762  GLfloat dot = v[0] * ctx->Transform.ClipEquation[p][0]
763  + v[1] * ctx->Transform.ClipEquation[p][1]
764  + v[2] * ctx->Transform.ClipEquation[p][2]
765  + v[3] * ctx->Transform.ClipEquation[p][3];
766  if (dot < 0.0F) {
767  return 0;
768  }
769  }
770  }
771 
772  return 1;
773 }
MAX_CLIP_PLANES
#define MAX_CLIP_PLANES
Definition: config.h:87
gl_context::Transform
struct gl_transform_attrib Transform
Definition: types.h:1335
v
const GLdouble * v
Definition: gl.h:2040
GLuint
unsigned int GLuint
Definition: gl.h:159
GLfloat
float GLfloat
Definition: gl.h:161
p
GLfloat GLfloat p
Definition: glext.h:8902
F
#define F(x, y, z)
Definition: md5.c:51

Referenced by gl_RasterPos4f().

◆ gl_userclip_polygon()

GLuint gl_userclip_polygon ( GLcontext *  ctx,
GLuint  n,
GLuint  vlist[] 
)

Definition at line 902 of file clip.c.

903 {
904  struct vertex_buffer* VB = ctx->VB;
905 
906  GLuint vlist2[VB_SIZE];
907  GLuint *inlist, *outlist;
908  GLuint incount, outcount;
909  GLuint curri, currj;
910  GLuint previ, prevj;
911  GLuint p;
912 
913  /* initialize input vertex list */
914  incount = n;
915  inlist = vlist;
916  outlist = vlist2;
917 
918  for (p=0;p<MAX_CLIP_PLANES;p++) {
919  if (ctx->Transform.ClipEnabled[p]) {
920  register float a = ctx->Transform.ClipEquation[p][0];
921  register float b = ctx->Transform.ClipEquation[p][1];
922  register float c = ctx->Transform.ClipEquation[p][2];
923  register float d = ctx->Transform.ClipEquation[p][3];
924 
925  if (incount<3) return 0;
926 
927  /* initialize prev to be last in the input list */
928  previ = incount - 1;
929  prevj = inlist[previ];
930 
931  outcount = 0;
932 
933  for (curri=0;curri<incount;curri++) {
934  currj = inlist[curri];
935 
936  if (INSIDE(currj, a,b,c,d)) {
937  if (INSIDE(prevj, a,b,c,d)) {
938  /* both verts are inside ==> copy current to outlist */
939  outlist[outcount++] = currj;
940  }
941  else {
942  /* current is inside and previous is outside ==> clip */
943  GLfloat dx, dy, dz, dw, t, denom;
944  /* compute t */
945  dx = VB->Eye[prevj][0] - VB->Eye[currj][0];
946  dy = VB->Eye[prevj][1] - VB->Eye[currj][1];
947  dz = VB->Eye[prevj][2] - VB->Eye[currj][2];
948  dw = VB->Eye[prevj][3] - VB->Eye[currj][3];
949  denom = dx*a + dy*b + dz*c + dw*d;
950  if (denom==0.0) {
951  t = 0.0;
952  }
953  else {
954  t = -(VB->Eye[currj][0]*a+VB->Eye[currj][1]*b
955  +VB->Eye[currj][2]*c+VB->Eye[currj][3]*d) / denom;
956  if (t>1.0F) {
957  t = 1.0F;
958  }
959  }
960  /* interpolate new vertex position */
961  VB->Eye[VB->Free][0] = VB->Eye[currj][0] + t*dx;
962  VB->Eye[VB->Free][1] = VB->Eye[currj][1] + t*dy;
963  VB->Eye[VB->Free][2] = VB->Eye[currj][2] + t*dz;
964  VB->Eye[VB->Free][3] = VB->Eye[currj][3] + t*dw;
965 
966  /* interpolate color, index, and/or texture coord */
967  if (ctx->ClipMask) {
968  interpolate_aux( ctx, EYE_SPACE, VB->Free, t, currj, prevj);
969  }
970  VB->Edgeflag[VB->Free] = VB->Edgeflag[prevj];
971 
972  /* output new vertex */
973  outlist[outcount++] = VB->Free;
974  VB->Free++;
975  if (VB->Free==VB_SIZE) VB->Free = 1;
976  /* output current vertex */
977  outlist[outcount++] = currj;
978  }
979  }
980  else {
981  if (INSIDE(prevj, a,b,c,d)) {
982  /* current is outside and previous is inside ==> clip */
983  GLfloat dx, dy, dz, dw, t, denom;
984  /* compute t */
985  dx = VB->Eye[currj][0]-VB->Eye[prevj][0];
986  dy = VB->Eye[currj][1]-VB->Eye[prevj][1];
987  dz = VB->Eye[currj][2]-VB->Eye[prevj][2];
988  dw = VB->Eye[currj][3]-VB->Eye[prevj][3];
989  denom = dx*a + dy*b + dz*c + dw*d;
990  if (denom==0.0) {
991  t = 0.0;
992  }
993  else {
994  t = -(VB->Eye[prevj][0]*a+VB->Eye[prevj][1]*b
995  +VB->Eye[prevj][2]*c+VB->Eye[prevj][3]*d) / denom;
996  if (t>1.0F) {
997  t = 1.0F;
998  }
999  }
1000  /* interpolate new vertex position */
1001  VB->Eye[VB->Free][0] = VB->Eye[prevj][0] + t*dx;
1002  VB->Eye[VB->Free][1] = VB->Eye[prevj][1] + t*dy;
1003  VB->Eye[VB->Free][2] = VB->Eye[prevj][2] + t*dz;
1004  VB->Eye[VB->Free][3] = VB->Eye[prevj][3] + t*dw;
1005 
1006  /* interpolate color, index, and/or texture coord */
1007  if (ctx->ClipMask) {
1008  interpolate_aux( ctx, EYE_SPACE, VB->Free, t, prevj, currj);
1009  }
1010  VB->Edgeflag[VB->Free] = VB->Edgeflag[prevj];
1011 
1012  /* output new vertex */
1013  outlist[outcount++] = VB->Free;
1014  VB->Free++;
1015  if (VB->Free==VB_SIZE) VB->Free = 1;
1016  }
1017  /* else both verts are outside ==> do nothing */
1018  }
1019 
1020  previ = curri;
1021  prevj = currj;
1022 
1023  /* check for overflowing vertex buffer */
1024  if (outcount>=VB_SIZE-1) {
1025  /* Too many vertices */
1026  if (outlist!=vlist2) {
1027  MEMCPY( vlist, vlist2, outcount * sizeof(GLuint) );
1028  }
1029  return VB_SIZE-1;
1030  }
1031 
1032  } /* for i */
1033 
1034  /* swap inlist and outlist pointers */
1035  {
1036  GLuint *tmp;
1037  tmp = inlist;
1038  inlist = outlist;
1039  outlist = tmp;
1040  incount = outcount;
1041  }
1042 
1043  } /* if */
1044  } /* for p */
1045 
1046  /* outlist points to the list of vertices resulting from the last */
1047  /* clipping. If outlist == vlist2 then we have to copy the vertices */
1048  /* back to vlist */
1049  if (outlist!=vlist2) {
1050  MEMCPY( vlist, vlist2, outcount * sizeof(GLuint) );
1051  }
1052 
1053  return outcount;
1054 }
EYE_SPACE
#define EYE_SPACE
Definition: clip.c:100
dy
GLint dy
Definition: linetemp.h:97
n
GLdouble n
Definition: glext.h:7729
t
GLdouble GLdouble t
Definition: gl.h:2047
gl_context::ClipMask
GLuint ClipMask
Definition: types.h:1359
interpolate_aux
void interpolate_aux(GLcontext *ctx, GLuint space, GLuint dst, GLfloat t, GLuint in, GLuint out)
Definition: clip.c:116
b
GLboolean GLboolean GLboolean b
Definition: glext.h:6204
MAX_CLIP_PLANES
#define MAX_CLIP_PLANES
Definition: config.h:87
d
#define d
Definition: ke_i.h:81
MEMCPY
#define MEMCPY(DST, SRC, BYTES)
Definition: macros.h:231
c
const GLubyte * c
Definition: glext.h:8905
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
gl_context::Transform
struct gl_transform_attrib Transform
Definition: types.h:1335
vertex_buffer
Definition: vb.h:99
VB
struct vertex_buffer * VB
Definition: tritemp.h:139
VB_SIZE
#define VB_SIZE
Definition: vb.h:89
GLuint
unsigned int GLuint
Definition: gl.h:159
INSIDE
#define INSIDE(K)
Definition: clip.c:780
dx
GLint dx
Definition: linetemp.h:97
GLfloat
float GLfloat
Definition: gl.h:161
a
GLboolean GLboolean GLboolean GLboolean a
Definition: glext.h:6204
p
GLfloat GLfloat p
Definition: glext.h:8902
gl_context::VB
struct vertex_buffer * VB
Definition: types.h:1380
F
#define F(x, y, z)
Definition: md5.c:51

Referenced by render_clipped_polygon().

◆ gl_viewclip_line()

GLuint gl_viewclip_line ( GLcontext *  ctx,
GLuint *  i,
GLuint *  j 
)

Definition at line 283 of file clip.c.

284 {
285  struct vertex_buffer* VB = ctx->VB;
286  GLfloat (*coord)[4] = VB->Clip;
287 
288  GLfloat t, dx, dy, dz, dw;
289  register GLuint ii, jj;
290 
291  ii = *i;
292  jj = *j;
293 
294 /*
295  * We use 6 instances of this code to clip agains the 6 planes.
296  * For each plane, we define the OUTSIDE and COMPUTE_INTERSECTION
297  * macros apprpriately.
298  */
299 #define GENERAL_CLIP \
300  if (OUTSIDE(ii)) { \
301  if (OUTSIDE(jj)) { \
302  /* both verts are outside ==> return 0 */ \
303  return 0; \
304  } \
305  else { \
306  /* ii is outside, jj is inside ==> clip */ \
307  /* new vertex put in position VB->Free */ \
308  COMPUTE_INTERSECTION( VB->Free, jj, ii ) \
309  if (ctx->ClipMask) \
310  ctx->ClipInterpAuxFunc( ctx, CLIP_SPACE, VB->Free, t, jj, ii );\
311  ii = VB->Free; \
312  VB->Free++; \
313  if (VB->Free==VB_SIZE) VB->Free = 1; \
314  } \
315  } \
316  else { \
317  if (OUTSIDE(jj)) { \
318  /* ii is inside, jj is outside ==> clip */ \
319  /* new vertex put in position VB->Free */ \
320  COMPUTE_INTERSECTION( VB->Free, ii, jj ); \
321  if (ctx->ClipMask) \
322  ctx->ClipInterpAuxFunc( ctx, CLIP_SPACE, VB->Free, t, ii, jj );\
323  jj = VB->Free; \
324  VB->Free++; \
325  if (VB->Free==VB_SIZE) VB->Free = 1; \
326  } \
327  /* else both verts are inside ==> do nothing */ \
328  }
329 
330 
331 #define X(I) coord[I][0]
332 #define Y(I) coord[I][1]
333 #define Z(I) coord[I][2]
334 #define W(I) coord[I][3]
335 
336 /*
337  * Begin clipping
338  */
339 
340  /*** Clip against +X side ***/
341 #define OUTSIDE(K) (X(K) > W(K))
342 #define COMPUTE_INTERSECTION( new, in, out ) \
343  dx = X(out) - X(in); \
344  dw = W(out) - W(in); \
345  t = (X(in) - W(in)) / (dw-dx); \
346  X(new) = X(in) + t * dx; \
347  Y(new) = Y(in) + t * (Y(out) - Y(in)); \
348  Z(new) = Z(in) + t * (Z(out) - Z(in)); \
349  W(new) = W(in) + t * dw;
350 
351  GENERAL_CLIP
352 
353 #undef OUTSIDE
354 #undef COMPUTE_INTERSECTION
355 
356 
357  /*** Clip against -X side ***/
358 #define OUTSIDE(K) (X(K) < -W(K))
359 #define COMPUTE_INTERSECTION( new, in, out ) \
360  dx = X(out) - X(in); \
361  dw = W(out) - W(in); \
362  t = -(X(in) + W(in)) / (dw+dx); \
363  X(new) = X(in) + t * dx; \
364  Y(new) = Y(in) + t * (Y(out) - Y(in)); \
365  Z(new) = Z(in) + t * (Z(out) - Z(in)); \
366  W(new) = W(in) + t * dw;
367 
368  GENERAL_CLIP
369 
370 #undef OUTSIDE
371 #undef COMPUTE_INTERSECTION
372 
373 
374  /*** Clip against +Y side ***/
375 #define OUTSIDE(K) (Y(K) > W(K))
376 #define COMPUTE_INTERSECTION( new, in, out ) \
377  dy = Y(out) - Y(in); \
378  dw = W(out) - W(in); \
379  t = (Y(in) - W(in)) / (dw-dy); \
380  X(new) = X(in) + t * (X(out) - X(in)); \
381  Y(new) = Y(in) + t * dy; \
382  Z(new) = Z(in) + t * (Z(out) - Z(in)); \
383  W(new) = W(in) + t * dw;
384 
385  GENERAL_CLIP
386 
387 #undef OUTSIDE
388 #undef COMPUTE_INTERSECTION
389 
390 
391  /*** Clip against -Y side ***/
392 #define OUTSIDE(K) (Y(K) < -W(K))
393 #define COMPUTE_INTERSECTION( new, in, out ) \
394  dy = Y(out) - Y(in); \
395  dw = W(out) - W(in); \
396  t = -(Y(in) + W(in)) / (dw+dy); \
397  X(new) = X(in) + t * (X(out) - X(in)); \
398  Y(new) = Y(in) + t * dy; \
399  Z(new) = Z(in) + t * (Z(out) - Z(in)); \
400  W(new) = W(in) + t * dw;
401 
402  GENERAL_CLIP
403 
404 #undef OUTSIDE
405 #undef COMPUTE_INTERSECTION
406 
407 
408  /*** Clip against +Z side ***/
409 #define OUTSIDE(K) (Z(K) > W(K))
410 #define COMPUTE_INTERSECTION( new, in, out ) \
411  dz = Z(out) - Z(in); \
412  dw = W(out) - W(in); \
413  t = (Z(in) - W(in)) / (dw-dz); \
414  X(new) = X(in) + t * (X(out) - X(in)); \
415  Y(new) = Y(in) + t * (Y(out) - Y(in)); \
416  Z(new) = Z(in) + t * dz; \
417  W(new) = W(in) + t * dw;
418 
419  GENERAL_CLIP
420 
421 #undef OUTSIDE
422 #undef COMPUTE_INTERSECTION
423 
424 
425  /*** Clip against -Z side ***/
426 #define OUTSIDE(K) (Z(K) < -W(K))
427 #define COMPUTE_INTERSECTION( new, in, out ) \
428  dz = Z(out) - Z(in); \
429  dw = W(out) - W(in); \
430  t = -(Z(in) + W(in)) / (dw+dz); \
431  X(new) = X(in) + t * (X(out) - X(in)); \
432  Y(new) = Y(in) + t * (Y(out) - Y(in)); \
433  Z(new) = Z(in) + t * dz; \
434  W(new) = W(in) + t * dw;
435 
436  GENERAL_CLIP
437 
438 #undef OUTSIDE
439 #undef COMPUTE_INTERSECTION
440 
441 #undef GENERAL_CLIP
442 
443  *i = ii;
444  *j = jj;
445  return 1;
446 }
GENERAL_CLIP
#define GENERAL_CLIP
dy
GLint dy
Definition: linetemp.h:97
t
GLdouble GLdouble t
Definition: gl.h:2047
coord
GLuint coord
Definition: glext.h:9511
i
GLsizei GLenum const GLvoid GLsizei GLenum GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLint GLint GLint GLshort GLshort GLshort GLubyte GLubyte GLubyte GLuint GLuint GLuint GLushort GLushort GLushort GLbyte GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLfloat GLint GLint GLint GLint GLshort GLshort GLshort GLshort GLubyte GLubyte GLubyte GLubyte GLuint GLuint GLuint GLuint GLushort GLushort GLushort GLushort GLboolean const GLdouble const GLfloat const GLint const GLshort const GLbyte const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLdouble const GLfloat const GLfloat const GLint const GLint const GLshort const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort GLenum GLenum GLenum GLfloat GLenum GLint GLenum GLenum GLenum GLfloat GLenum GLenum GLint GLenum GLfloat GLenum GLint GLint GLushort GLenum GLenum GLfloat GLenum GLenum GLint GLfloat const GLubyte GLenum GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLint GLint GLsizei GLsizei GLint GLenum GLenum const GLvoid GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLenum const GLdouble GLenum GLenum const GLfloat GLenum GLenum const GLint GLsizei GLuint GLfloat GLuint GLbitfield GLfloat GLint GLuint GLboolean GLenum GLfloat GLenum GLbitfield GLenum GLfloat GLfloat GLint GLint const GLfloat GLenum GLfloat GLfloat GLint GLint GLfloat GLfloat GLint GLint const GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat const GLdouble const GLfloat const GLdouble const GLfloat GLint i
Definition: glfuncs.h:248
j
GLsizei GLenum const GLvoid GLsizei GLenum GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLint GLint GLint GLshort GLshort GLshort GLubyte GLubyte GLubyte GLuint GLuint GLuint GLushort GLushort GLushort GLbyte GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLfloat GLint GLint GLint GLint GLshort GLshort GLshort GLshort GLubyte GLubyte GLubyte GLubyte GLuint GLuint GLuint GLuint GLushort GLushort GLushort GLushort GLboolean const GLdouble const GLfloat const GLint const GLshort const GLbyte const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLdouble const GLfloat const GLfloat const GLint const GLint const GLshort const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort GLenum GLenum GLenum GLfloat GLenum GLint GLenum GLenum GLenum GLfloat GLenum GLenum GLint GLenum GLfloat GLenum GLint GLint GLushort GLenum GLenum GLfloat GLenum GLenum GLint GLfloat const GLubyte GLenum GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLint GLint GLsizei GLsizei GLint GLenum GLenum const GLvoid GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLenum const GLdouble GLenum GLenum const GLfloat GLenum GLenum const GLint GLsizei GLuint GLfloat GLuint GLbitfield GLfloat GLint GLuint GLboolean GLenum GLfloat GLenum GLbitfield GLenum GLfloat GLfloat GLint GLint const GLfloat GLenum GLfloat GLfloat GLint GLint GLfloat GLfloat GLint GLint const GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat const GLdouble const GLfloat const GLdouble const GLfloat GLint GLint GLint j
Definition: glfuncs.h:250
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
vertex_buffer
Definition: vb.h:99
VB
struct vertex_buffer * VB
Definition: tritemp.h:139
GLuint
unsigned int GLuint
Definition: gl.h:159
dx
GLint dx
Definition: linetemp.h:97
GLfloat
float GLfloat
Definition: gl.h:161
gl_context::VB
struct vertex_buffer * VB
Definition: types.h:1380

Referenced by render_clipped_line().

◆ gl_viewclip_point()

GLuint gl_viewclip_point ( const GLfloat  v[])

Definition at line 262 of file clip.c.

263 {
264  if ( v[0] > v[3] || v[0] < -v[3]
265  || v[1] > v[3] || v[1] < -v[3]
266  || v[2] > v[3] || v[2] < -v[3] ) {
267  return 0;
268  }
269  else {
270  return 1;
271  }
272 }
v
const GLdouble * v
Definition: gl.h:2040

Referenced by gl_RasterPos4f().

◆ gl_viewclip_polygon()

GLuint gl_viewclip_polygon ( GLcontext *  ctx,
GLuint  n,
GLuint  vlist[] 
)

Definition at line 458 of file clip.c.

460 {
461  struct vertex_buffer* VB = ctx->VB;
462  GLfloat (*coord)[4] = VB->Clip;
463 
464  GLuint previ, prevj;
465  GLuint curri, currj;
466  GLuint vlist2[VB_SIZE];
467  GLuint n2;
468  GLdouble dx, dy, dz, dw, t, neww;
469 
470 /*
471  * We use 6 instances of this code to implement clipping against the
472  * 6 sides of the view volume. Prior to each we define the macros:
473  * INLIST = array which lists input vertices
474  * OUTLIST = array which lists output vertices
475  * INCOUNT = variable which is the number of vertices in INLIST[]
476  * OUTCOUNT = variable which is the number of vertices in OUTLIST[]
477  * INSIDE(i) = test if vertex v[i] is inside the view volume
478  * COMPUTE_INTERSECTION(in,out,new) = compute intersection of line
479  * from v[in] to v[out] with the clipping plane and store
480  * the result in v[new]
481  */
482 
483 #define GENERAL_CLIP \
484  if (INCOUNT<3) return 0; \
485  previ = INCOUNT-1; /* let previous = last vertex */ \
486  prevj = INLIST[previ]; \
487  OUTCOUNT = 0; \
488  for (curri=0;curri<INCOUNT;curri++) { \
489  currj = INLIST[curri]; \
490  if (INSIDE(currj)) { \
491  if (INSIDE(prevj)) { \
492  /* both verts are inside ==> copy current to outlist */ \
493  OUTLIST[OUTCOUNT] = currj; \
494  OUTCOUNT++; \
495  } \
496  else { \
497  /* current is inside and previous is outside ==> clip */ \
498  COMPUTE_INTERSECTION( currj, prevj, VB->Free ) \
499  /* if new point not coincident with previous point... */ \
500  if (t>0.0) { \
501  /* interpolate aux info using the value of t */ \
502  if (ctx->ClipMask) \
503  ctx->ClipInterpAuxFunc( ctx, CLIP_SPACE, VB->Free, t, currj, prevj ); \
504  VB->Edgeflag[VB->Free] = VB->Edgeflag[prevj]; \
505  /* output new point */ \
506  OUTLIST[OUTCOUNT] = VB->Free; \
507  VB->Free++; \
508  if (VB->Free==VB_SIZE) VB->Free = 1; \
509  OUTCOUNT++; \
510  } \
511  /* Output current */ \
512  OUTLIST[OUTCOUNT] = currj; \
513  OUTCOUNT++; \
514  } \
515  } \
516  else { \
517  if (INSIDE(prevj)) { \
518  /* current is outside and previous is inside ==> clip */ \
519  COMPUTE_INTERSECTION( prevj, currj, VB->Free ) \
520  /* if new point not coincident with previous point... */ \
521  if (t>0.0) { \
522  /* interpolate aux info using the value of t */ \
523  if (ctx->ClipMask) \
524  ctx->ClipInterpAuxFunc( ctx, CLIP_SPACE, VB->Free, t, prevj, currj ); \
525  VB->Edgeflag[VB->Free] = VB->Edgeflag[prevj]; \
526  /* output new point */ \
527  OUTLIST[OUTCOUNT] = VB->Free; \
528  VB->Free++; \
529  if (VB->Free==VB_SIZE) VB->Free = 1; \
530  OUTCOUNT++; \
531  } \
532  } \
533  /* else both verts are outside ==> do nothing */ \
534  } \
535  /* let previous = current */ \
536  previ = curri; \
537  prevj = currj; \
538  /* check for overflowing vertex buffer */ \
539  if (OUTCOUNT>=VB_SIZE-1) { \
540  /* Too many vertices */ \
541  if (OUTLIST==vlist2) { \
542  /* copy OUTLIST[] to vlist[] */ \
543  int i; \
544  for (i=0;i<VB_SIZE;i++) { \
545  vlist[i] = OUTLIST[i]; \
546  } \
547  } \
548  return VB_SIZE-1; \
549  } \
550  }
551 
552 
553 #define X(I) coord[I][0]
554 #define Y(I) coord[I][1]
555 #define Z(I) coord[I][2]
556 #define W(I) coord[I][3]
557 
558 /*
559  * Clip against +X
560  */
561 #define INCOUNT n
562 #define OUTCOUNT n2
563 #define INLIST vlist
564 #define OUTLIST vlist2
565 #define INSIDE(K) (X(K) <= W(K))
566 
567 #define COMPUTE_INTERSECTION( in, out, new ) \
568  dx = X(out) - X(in); \
569  dw = W(out) - W(in); \
570  t = (X(in)-W(in)) / (dw-dx); \
571  neww = W(in) + t * dw; \
572  X(new) = neww; \
573  Y(new) = Y(in) + t * (Y(out) - Y(in)); \
574  Z(new) = Z(in) + t * (Z(out) - Z(in)); \
575  W(new) = neww;
576 
577  GENERAL_CLIP
578 
579 #undef INCOUNT
580 #undef OUTCOUNT
581 #undef INLIST
582 #undef OUTLIST
583 #undef INSIDE
584 #undef COMPUTE_INTERSECTION
585 
586 
587 /*
588  * Clip against -X
589  */
590 #define INCOUNT n2
591 #define OUTCOUNT n
592 #define INLIST vlist2
593 #define OUTLIST vlist
594 #define INSIDE(K) (X(K) >= -W(K))
595 #define COMPUTE_INTERSECTION( in, out, new ) \
596  dx = X(out)-X(in); \
597  dw = W(out)-W(in); \
598  t = -(X(in)+W(in)) / (dw+dx); \
599  neww = W(in) + t * dw; \
600  X(new) = -neww; \
601  Y(new) = Y(in) + t * (Y(out) - Y(in)); \
602  Z(new) = Z(in) + t * (Z(out) - Z(in)); \
603  W(new) = neww;
604 
605  GENERAL_CLIP
606 
607 #undef INCOUNT
608 #undef OUTCOUNT
609 #undef INLIST
610 #undef OUTLIST
611 #undef INSIDE
612 #undef COMPUTE_INTERSECTION
613 
614 
615 /*
616  * Clip against +Y
617  */
618 #define INCOUNT n
619 #define OUTCOUNT n2
620 #define INLIST vlist
621 #define OUTLIST vlist2
622 #define INSIDE(K) (Y(K) <= W(K))
623 #define COMPUTE_INTERSECTION( in, out, new ) \
624  dy = Y(out)-Y(in); \
625  dw = W(out)-W(in); \
626  t = (Y(in)-W(in)) / (dw-dy); \
627  neww = W(in) + t * dw; \
628  X(new) = X(in) + t * (X(out) - X(in)); \
629  Y(new) = neww; \
630  Z(new) = Z(in) + t * (Z(out) - Z(in)); \
631  W(new) = neww;
632 
633  GENERAL_CLIP
634 
635 #undef INCOUNT
636 #undef OUTCOUNT
637 #undef INLIST
638 #undef OUTLIST
639 #undef INSIDE
640 #undef COMPUTE_INTERSECTION
641 
642 
643 /*
644  * Clip against -Y
645  */
646 #define INCOUNT n2
647 #define OUTCOUNT n
648 #define INLIST vlist2
649 #define OUTLIST vlist
650 #define INSIDE(K) (Y(K) >= -W(K))
651 #define COMPUTE_INTERSECTION( in, out, new ) \
652  dy = Y(out)-Y(in); \
653  dw = W(out)-W(in); \
654  t = -(Y(in)+W(in)) / (dw+dy); \
655  neww = W(in) + t * dw; \
656  X(new) = X(in) + t * (X(out) - X(in)); \
657  Y(new) = -neww; \
658  Z(new) = Z(in) + t * (Z(out) - Z(in)); \
659  W(new) = neww;
660 
661  GENERAL_CLIP
662 
663 #undef INCOUNT
664 #undef OUTCOUNT
665 #undef INLIST
666 #undef OUTLIST
667 #undef INSIDE
668 #undef COMPUTE_INTERSECTION
669 
670 
671 
672 /*
673  * Clip against +Z
674  */
675 #define INCOUNT n
676 #define OUTCOUNT n2
677 #define INLIST vlist
678 #define OUTLIST vlist2
679 #define INSIDE(K) (Z(K) <= W(K))
680 #define COMPUTE_INTERSECTION( in, out, new ) \
681  dz = Z(out)-Z(in); \
682  dw = W(out)-W(in); \
683  t = (Z(in)-W(in)) / (dw-dz); \
684  neww = W(in) + t * dw; \
685  X(new) = X(in) + t * (X(out) - X(in)); \
686  Y(new) = Y(in) + t * (Y(out) - Y(in)); \
687  Z(new) = neww; \
688  W(new) = neww;
689 
690  GENERAL_CLIP
691 
692 #undef INCOUNT
693 #undef OUTCOUNT
694 #undef INLIST
695 #undef OUTLIST
696 #undef INSIDE
697 #undef COMPUTE_INTERSECTION
698 
699 
700 /*
701  * Clip against -Z
702  */
703 #define INCOUNT n2
704 #define OUTCOUNT n
705 #define INLIST vlist2
706 #define OUTLIST vlist
707 #define INSIDE(K) (Z(K) >= -W(K))
708 #define COMPUTE_INTERSECTION( in, out, new ) \
709  dz = Z(out)-Z(in); \
710  dw = W(out)-W(in); \
711  t = -(Z(in)+W(in)) / (dw+dz); \
712  neww = W(in) + t * dw; \
713  X(new) = X(in) + t * (X(out) - X(in)); \
714  Y(new) = Y(in) + t * (Y(out) - Y(in)); \
715  Z(new) = -neww; \
716  W(new) = neww;
717 
718  GENERAL_CLIP
719 
720 #undef INCOUNT
721 #undef INLIST
722 #undef OUTLIST
723 #undef INSIDE
724 #undef COMPUTE_INTERSECTION
725 
726  /* 'OUTCOUNT' clipped vertices are now back in v[] */
727  return OUTCOUNT;
728 
729 #undef GENERAL_CLIP
730 #undef OUTCOUNT
731 }
GLdouble
double GLdouble
Definition: gl.h:163
GENERAL_CLIP
#define GENERAL_CLIP
dy
GLint dy
Definition: linetemp.h:97
t
GLdouble GLdouble t
Definition: gl.h:2047
coord
GLuint coord
Definition: glext.h:9511
dw
REFIID LPVOID DWORD dw
Definition: atlbase.h:40
vertex_buffer
Definition: vb.h:99
VB
struct vertex_buffer * VB
Definition: tritemp.h:139
VB_SIZE
#define VB_SIZE
Definition: vb.h:89
GLuint
unsigned int GLuint
Definition: gl.h:159
n2
int n2
Definition: dwarfget.c:148
OUTCOUNT
#define OUTCOUNT
dx
GLint dx
Definition: linetemp.h:97
GLfloat
float GLfloat
Definition: gl.h:161
gl_context::VB
struct vertex_buffer * VB
Definition: types.h:1380

Referenced by render_clipped_polygon().

◆ interpolate_aux()

void interpolate_aux ( GLcontext *  ctx,
GLuint  space,
GLuint  dst,
GLfloat  t,
GLuint  in,
GLuint  out 
)

Definition at line 116 of file clip.c.

118 {
119  struct vertex_buffer* VB = ctx->VB;
120 
121  if (ctx->ClipMask & CLIP_FCOLOR_BIT) {
122  VB->Fcolor[dst][0] = LINTERP( t, VB->Fcolor[in][0], VB->Fcolor[out][0] );
123  VB->Fcolor[dst][1] = LINTERP( t, VB->Fcolor[in][1], VB->Fcolor[out][1] );
124  VB->Fcolor[dst][2] = LINTERP( t, VB->Fcolor[in][2], VB->Fcolor[out][2] );
125  VB->Fcolor[dst][3] = LINTERP( t, VB->Fcolor[in][3], VB->Fcolor[out][3] );
126  }
127  else if (ctx->ClipMask & CLIP_FINDEX_BIT) {
128  VB->Findex[dst] = (GLuint) (GLint) LINTERP( t, (GLfloat) VB->Findex[in],
129  (GLfloat) VB->Findex[out] );
130  }
131 
132  if (ctx->ClipMask & CLIP_BCOLOR_BIT) {
133  VB->Bcolor[dst][0] = LINTERP( t, VB->Bcolor[in][0], VB->Bcolor[out][0] );
134  VB->Bcolor[dst][1] = LINTERP( t, VB->Bcolor[in][1], VB->Bcolor[out][1] );
135  VB->Bcolor[dst][2] = LINTERP( t, VB->Bcolor[in][2], VB->Bcolor[out][2] );
136  VB->Bcolor[dst][3] = LINTERP( t, VB->Bcolor[in][3], VB->Bcolor[out][3] );
137  }
138  else if (ctx->ClipMask & CLIP_BINDEX_BIT) {
139  VB->Bindex[dst] = (GLuint) (GLint) LINTERP( t, (GLfloat) VB->Bindex[in],
140  (GLfloat) VB->Bindex[out] );
141  }
142 
143  if (ctx->ClipMask & CLIP_TEXTURE_BIT) {
144  /* TODO: is more sophisticated texture coord interpolation needed?? */
145  if (space==CLIP_SPACE) {
146  /* also interpolate eye Z component */
147  VB->Eye[dst][2] = LINTERP( t, VB->Eye[in][2], VB->Eye[out][2] );
148  }
149  VB->TexCoord[dst][0] = LINTERP(t,VB->TexCoord[in][0],VB->TexCoord[out][0]);
150  VB->TexCoord[dst][1] = LINTERP(t,VB->TexCoord[in][1],VB->TexCoord[out][1]);
151  VB->TexCoord[dst][2] = LINTERP(t,VB->TexCoord[in][2],VB->TexCoord[out][2]);
152  VB->TexCoord[dst][3] = LINTERP(t,VB->TexCoord[in][3],VB->TexCoord[out][3]);
153  }
154 
155 }
CLIP_TEXTURE_BIT
#define CLIP_TEXTURE_BIT
Definition: types.h:1208
t
GLdouble GLdouble t
Definition: gl.h:2047
gl_context::ClipMask
GLuint ClipMask
Definition: types.h:1359
CLIP_FCOLOR_BIT
#define CLIP_FCOLOR_BIT
Definition: types.h:1204
LINTERP
#define LINTERP(T, A, B)
Definition: clip.c:96
CLIP_BINDEX_BIT
#define CLIP_BINDEX_BIT
Definition: types.h:1207
out
static FILE * out
Definition: regtests2xml.c:44
vertex_buffer
Definition: vb.h:99
VB
struct vertex_buffer * VB
Definition: tritemp.h:139
GLuint
unsigned int GLuint
Definition: gl.h:159
CLIP_BCOLOR_BIT
#define CLIP_BCOLOR_BIT
Definition: types.h:1205
in
GLuint in
Definition: glext.h:9616
dst
GLenum GLenum dst
Definition: glext.h:6340
GLfloat
float GLfloat
Definition: gl.h:161
CLIP_FINDEX_BIT
#define CLIP_FINDEX_BIT
Definition: types.h:1206
GLint
int GLint
Definition: gl.h:156
gl_context::VB
struct vertex_buffer * VB
Definition: types.h:1380
CLIP_SPACE
#define CLIP_SPACE
Definition: clip.c:101

Referenced by gl_userclip_line(), gl_userclip_polygon(), and update_clipmask().

◆ interpolate_aux_color()

void interpolate_aux_color ( GLcontext *  ctx,
GLuint  space,
GLuint  dst,
GLfloat  t,
GLuint  in,
GLuint  out 
)

Definition at line 190 of file clip.c.

192 {
193  struct vertex_buffer* VB = ctx->VB;
194 
195  VB->Fcolor[dst][0] = LINTERP( t, VB->Fcolor[in][0], VB->Fcolor[out][0] );
196  VB->Fcolor[dst][1] = LINTERP( t, VB->Fcolor[in][1], VB->Fcolor[out][1] );
197  VB->Fcolor[dst][2] = LINTERP( t, VB->Fcolor[in][2], VB->Fcolor[out][2] );
198  VB->Fcolor[dst][3] = LINTERP( t, VB->Fcolor[in][3], VB->Fcolor[out][3] );
199 }
t
GLdouble GLdouble t
Definition: gl.h:2047
LINTERP
#define LINTERP(T, A, B)
Definition: clip.c:96
out
static FILE * out
Definition: regtests2xml.c:44
vertex_buffer
Definition: vb.h:99
VB
struct vertex_buffer * VB
Definition: tritemp.h:139
in
GLuint in
Definition: glext.h:9616
dst
GLenum GLenum dst
Definition: glext.h:6340
gl_context::VB
struct vertex_buffer * VB
Definition: types.h:1380

Referenced by update_clipmask().

◆ interpolate_aux_color_tex2()

void interpolate_aux_color_tex2 ( GLcontext *  ctx,
GLuint  space,
GLuint  dst,
GLfloat  t,
GLuint  in,
GLuint  out 
)

Definition at line 163 of file clip.c.

165 {
166  struct vertex_buffer* VB = ctx->VB;
167 
168  VB->Fcolor[dst][0] = LINTERP( t, VB->Fcolor[in][0], VB->Fcolor[out][0] );
169  VB->Fcolor[dst][1] = LINTERP( t, VB->Fcolor[in][1], VB->Fcolor[out][1] );
170  VB->Fcolor[dst][2] = LINTERP( t, VB->Fcolor[in][2], VB->Fcolor[out][2] );
171  VB->Fcolor[dst][3] = LINTERP( t, VB->Fcolor[in][3], VB->Fcolor[out][3] );
172 
173  VB->Eye[dst][2] = LINTERP( t, VB->Eye[in][2], VB->Eye[out][2] );
174  VB->TexCoord[dst][0] = LINTERP(t,VB->TexCoord[in][0],VB->TexCoord[out][0]);
175  VB->TexCoord[dst][1] = LINTERP(t,VB->TexCoord[in][1],VB->TexCoord[out][1]);
176 }
t
GLdouble GLdouble t
Definition: gl.h:2047
LINTERP
#define LINTERP(T, A, B)
Definition: clip.c:96
out
static FILE * out
Definition: regtests2xml.c:44
vertex_buffer
Definition: vb.h:99
VB
struct vertex_buffer * VB
Definition: tritemp.h:139
in
GLuint in
Definition: glext.h:9616
dst
GLenum GLenum dst
Definition: glext.h:6340
gl_context::VB
struct vertex_buffer * VB
Definition: types.h:1380

Referenced by update_clipmask().

◆ interpolate_aux_tex2()

void interpolate_aux_tex2 ( GLcontext *  ctx,
GLuint  space,
GLuint  dst,
GLfloat  t,
GLuint  in,
GLuint  out 
)

Definition at line 179 of file clip.c.

181 {
182  struct vertex_buffer* VB = ctx->VB;
183 
184  VB->Eye[dst][2] = LINTERP( t, VB->Eye[in][2], VB->Eye[out][2] );
185  VB->TexCoord[dst][0] = LINTERP(t,VB->TexCoord[in][0],VB->TexCoord[out][0]);
186  VB->TexCoord[dst][1] = LINTERP(t,VB->TexCoord[in][1],VB->TexCoord[out][1]);
187 }
t
GLdouble GLdouble t
Definition: gl.h:2047
LINTERP
#define LINTERP(T, A, B)
Definition: clip.c:96
out
static FILE * out
Definition: regtests2xml.c:44
vertex_buffer
Definition: vb.h:99
VB
struct vertex_buffer * VB
Definition: tritemp.h:139
in
GLuint in
Definition: glext.h:9616
dst
GLenum GLenum dst
Definition: glext.h:6340
gl_context::VB
struct vertex_buffer * VB
Definition: types.h:1380

Referenced by update_clipmask().