matrix.c File Reference

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "context.h"
#include "dlist.h"
#include "macros.h"
#include "matrix.h"
#include "mmath.h"
#include "types.h"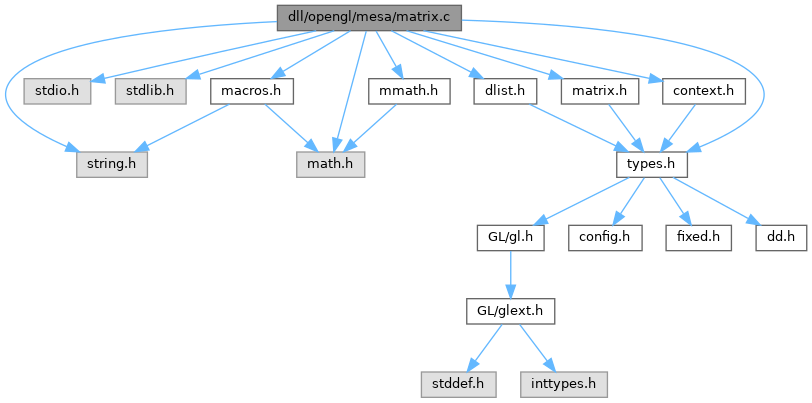

Include dependency graph for matrix.c:

Go to the source code of this file.

Macros
#define	A(row, col)   a[(col<<2)+row]
#define	B(row, col)   b[(col<<2)+row]
#define	P(row, col)   product[(col<<2)+row]
#define	MAT(m, r, c)   (m)[(c)*4+(r)]
#define	m11   MAT(m,0,0)
#define	m12   MAT(m,0,1)
#define	m13   MAT(m,0,2)
#define	m14   MAT(m,0,3)
#define	m21   MAT(m,1,0)
#define	m22   MAT(m,1,1)
#define	m23   MAT(m,1,2)
#define	m24   MAT(m,1,3)
#define	m31   MAT(m,2,0)
#define	m32   MAT(m,2,1)
#define	m33   MAT(m,2,2)
#define	m34   MAT(m,2,3)
#define	m41   MAT(m,3,0)
#define	m42   MAT(m,3,1)
#define	m43   MAT(m,3,2)
#define	m44   MAT(m,3,3)
#define	M(row, col)   m[col*4+row]
#define	M(row, col)   m[col*4+row]
#define	M(row, col)   m[col*4+row]
#define	M(row, col)   m[col*4+row]

Typedefs
typedef GLfloat	Mat2[2][2]

Enumerations
enum	{   M00 = 0 , M01 = 4 , M02 = 8 , M03 = 12 ,   M10 = 1 , M11 = 5 , M12 = 9 , M13 = 13 ,   M20 = 2 , M21 = 6 , M22 = 10 , M23 = 14 ,   M30 = 3 , M31 = 7 , M32 = 11 , M33 = 15 }

Functions
static void	matmul (GLfloat *product, const GLfloat *a, const GLfloat *b)
static void	invert_matrix_general (const GLfloat *m, GLfloat *out)
static void	invert_matrix (const GLfloat *m, GLfloat *out)
static GLboolean	is_identity (const GLfloat m[16])
void	gl_analyze_modelview_matrix (GLcontext *ctx)
void	gl_analyze_projection_matrix (GLcontext *ctx)
void	gl_analyze_texture_matrix (GLcontext *ctx)
void	gl_Frustum (GLcontext *ctx, GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble nearval, GLdouble farval)
void	gl_Ortho (GLcontext *ctx, GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble nearval, GLdouble farval)
void	gl_MatrixMode (GLcontext *ctx, GLenum mode)
void	gl_PushMatrix (GLcontext *ctx)
void	gl_PopMatrix (GLcontext *ctx)
void	gl_LoadIdentity (GLcontext *ctx)
void	gl_LoadMatrixf (GLcontext *ctx, const GLfloat *m)
void	gl_MultMatrixf (GLcontext *ctx, const GLfloat *m)
void	gl_rotation_matrix (GLfloat angle, GLfloat x, GLfloat y, GLfloat z, GLfloat m[])
void	gl_Rotatef (GLcontext *ctx, GLfloat angle, GLfloat x, GLfloat y, GLfloat z)
void	gl_Scalef (GLcontext *ctx, GLfloat x, GLfloat y, GLfloat z)
void	gl_Translatef (GLcontext *ctx, GLfloat x, GLfloat y, GLfloat z)
void	gl_Viewport (GLcontext *ctx, GLint x, GLint y, GLsizei width, GLsizei height)

Variables
static GLfloat	Identity [16]

Macro Definition Documentation

A

#define A	(		row,
			col
	)		a[(col<<2)+row]

B

#define B	(		row,
			col
	)		b[(col<<2)+row]

M [1/4]

#define M	(		row,
			col
	)		m[col*4+row]

M [2/4]

#define M	(		row,
			col
	)		m[col*4+row]

M [3/4]

#define M	(		row,
			col
	)		m[col*4+row]

M [4/4]

#define M	(		row,
			col
	)		m[col*4+row]

m11

#define m11   MAT(m,0,0)

m12

#define m12   MAT(m,0,1)

m13

#define m13   MAT(m,0,2)

m14

#define m14   MAT(m,0,3)

m21

#define m21   MAT(m,1,0)

m22

#define m22   MAT(m,1,1)

m23

#define m23   MAT(m,1,2)

m24

#define m24   MAT(m,1,3)

m31

#define m31   MAT(m,2,0)

m32

#define m32   MAT(m,2,1)

m33

#define m33   MAT(m,2,2)

m34

#define m34   MAT(m,2,3)

m41

#define m41   MAT(m,3,0)

m42

#define m42   MAT(m,3,1)

m43

#define m43   MAT(m,3,2)

m44

#define m44   MAT(m,3,3)

MAT

#define MAT	(		m,
			r,
			c
	)		(m)[(c)*4+(r)]

P

#define P	(		row,
			col
	)		product[(col<<2)+row]

Typedef Documentation

Mat2

typedef GLfloat Mat2[2][2]

Definition at line 190 of file matrix.c.

Enumeration Type Documentation

anonymous enum

anonymous enum

Enumerator
M00
M01
M02
M03
M10
M11
M12
M13
M20
M21
M22
M23
M30
M31
M32
M33

Definition at line 192 of file matrix.c.

     {
    M00 = 0, M01 = 4, M02 = 8, M03 = 12,
    M10 = 1, M11 = 5, M12 = 9, M13 = 13,
    M20 = 2, M21 = 6, M22 = 10,M23 = 14,
    M30 = 3, M31 = 7, M32 = 11,M33 = 15
};

Function Documentation

gl_analyze_modelview_matrix()

void gl_analyze_modelview_matrix

(

GLcontext *

ctx

)

Definition at line 420 of file matrix.c.

{
   const GLfloat *m = ctx->ModelViewMatrix;
   if (is_identity(m)) {
      ctx->ModelViewMatrixType = MATRIX_IDENTITY;
   }
   else if (                 m[4]==0.0F && m[ 8]==0.0F               
            && m[1]==0.0F               && m[ 9]==0.0F
            && m[2]==0.0F && m[6]==0.0F && m[10]==1.0F && m[14]==0.0F
            && m[3]==0.0F && m[7]==0.0F && m[11]==0.0F && m[15]==1.0F) {
      ctx->ModelViewMatrixType = MATRIX_2D_NO_ROT;
   }
   else if (                               m[ 8]==0.0F               
            &&                             m[ 9]==0.0F
            && m[2]==0.0F && m[6]==0.0F && m[10]==1.0F && m[14]==0.0F
            && m[3]==0.0F && m[7]==0.0F && m[11]==0.0F && m[15]==1.0F) {
      ctx->ModelViewMatrixType = MATRIX_2D;
   }
   else if (m[3]==0.0F && m[7]==0.0F && m[11]==0.0F && m[15]==1.0F) {
      ctx->ModelViewMatrixType = MATRIX_3D;
   }
   else {
      ctx->ModelViewMatrixType = MATRIX_GENERAL;
   }
 
   invert_matrix( ctx->ModelViewMatrix, ctx->ModelViewInv );
   ctx->NewModelViewMatrix = GL_FALSE;
}

Referenced by gl_Begin(), gl_ClipPlane(), gl_Lightfv(), gl_RasterPos4f(), gl_TexGenfv(), and gl_windowpos().

gl_analyze_projection_matrix()

void gl_analyze_projection_matrix

(

GLcontext *

ctx

)

Definition at line 455 of file matrix.c.

{
   /* look for common-case ortho and perspective matrices */
   const GLfloat *m = ctx->ProjectionMatrix;
   if (is_identity(m)) {
      ctx->ProjectionMatrixType = MATRIX_IDENTITY;
   }
   else if (                 m[4]==0.0F && m[8] ==0.0F
            && m[1]==0.0F               && m[9] ==0.0F
            && m[2]==0.0F && m[6]==0.0F
            && m[3]==0.0F && m[7]==0.0F && m[11]==0.0F && m[15]==1.0F) {
      ctx->ProjectionMatrixType = MATRIX_ORTHO;
   }
   else if (                 m[4]==0.0F                 && m[12]==0.0F
            && m[1]==0.0F                               && m[13]==0.0F
            && m[2]==0.0F && m[6]==0.0F
            && m[3]==0.0F && m[7]==0.0F && m[11]==-1.0F && m[15]==0.0F) {
      ctx->ProjectionMatrixType = MATRIX_PERSPECTIVE;
   }
   else {
      ctx->ProjectionMatrixType = MATRIX_GENERAL;
   }
 
   ctx->NewProjectionMatrix = GL_FALSE;
}

Referenced by gl_Begin(), and gl_RasterPos4f().

gl_analyze_texture_matrix()

void gl_analyze_texture_matrix

(

GLcontext *

ctx

)

Definition at line 487 of file matrix.c.

{
   const GLfloat *m = ctx->TextureMatrix;
   if (is_identity(m)) {
      ctx->TextureMatrixType = MATRIX_IDENTITY;
   }
   else if (                               m[ 8]==0.0F               
            &&                             m[ 9]==0.0F
            && m[2]==0.0F && m[6]==0.0F && m[10]==1.0F && m[14]==0.0F
            && m[3]==0.0F && m[7]==0.0F && m[11]==0.0F && m[15]==1.0F) {
      ctx->TextureMatrixType = MATRIX_2D;
   }
   else if (m[3]==0.0F && m[7]==0.0F && m[11]==0.0F && m[15]==1.0F) {
      ctx->TextureMatrixType = MATRIX_3D;
   }
   else {
      ctx->TextureMatrixType = MATRIX_GENERAL;
   }
 
   ctx->NewTextureMatrix = GL_FALSE;
}

Referenced by gl_RasterPos4f(), and gl_transform_vb_part2().

gl_Frustum()

void gl_Frustum	(	GLcontext *	ctx,
		GLdouble	left,
		GLdouble	right,
		GLdouble	bottom,
		GLdouble	top,
		GLdouble	nearval,
		GLdouble	farval
	)

Definition at line 511 of file matrix.c.

{
   GLfloat x, y, a, b, c, d;
   GLfloat m[16];
 
   if (nearval<=0.0 || farval<=0.0) {
      gl_error( ctx,  GL_INVALID_VALUE, "glFrustum(near or far)" );
   }
 
   x = (2.0*nearval) / (right-left);
   y = (2.0*nearval) / (top-bottom);
   a = (right+left) / (right-left);
   b = (top+bottom) / (top-bottom);
   c = -(farval+nearval) / ( farval-nearval);
   d = -(2.0*farval*nearval) / (farval-nearval);  /* error? */
 
#define M(row,col)  m[col*4+row]
   M(0,0) = x;     M(0,1) = 0.0F;  M(0,2) = a;      M(0,3) = 0.0F;
   M(1,0) = 0.0F;  M(1,1) = y;     M(1,2) = b;      M(1,3) = 0.0F;
   M(2,0) = 0.0F;  M(2,1) = 0.0F;  M(2,2) = c;      M(2,3) = d;
   M(3,0) = 0.0F;  M(3,1) = 0.0F;  M(3,2) = -1.0F;  M(3,3) = 0.0F;
#undef M
 
   gl_MultMatrixf( ctx, m );
 
 
   /* Need to keep a stack of near/far values in case the user push/pops
    * the projection matrix stack so that we can call Driver.NearFar()
    * after a pop.
    */
   ctx->NearFarStack[ctx->ProjectionStackDepth][0] = nearval;
   ctx->NearFarStack[ctx->ProjectionStackDepth][1] = farval;
 
   if (ctx->Driver.NearFar) {
      (*ctx->Driver.NearFar)( ctx, nearval, farval );
   }
}

Referenced by execute_list(), and init_exec_pointers().

gl_LoadIdentity()

void gl_LoadIdentity

(

GLcontext *

ctx

)

Definition at line 709 of file matrix.c.

{
   if (INSIDE_BEGIN_END(ctx)) {
      gl_error( ctx,  GL_INVALID_OPERATION, "glLoadIdentity" );
      return;
   }
   switch (ctx->Transform.MatrixMode) {
      case GL_MODELVIEW:
         MEMCPY( ctx->ModelViewMatrix, Identity, 16*sizeof(GLfloat) );
         MEMCPY( ctx->ModelViewInv, Identity, 16*sizeof(GLfloat) );
         ctx->ModelViewMatrixType = MATRIX_IDENTITY;
     ctx->NewModelViewMatrix = GL_FALSE;
     break;
      case GL_PROJECTION:
     MEMCPY( ctx->ProjectionMatrix, Identity, 16*sizeof(GLfloat) );
         ctx->ProjectionMatrixType = MATRIX_IDENTITY;
     ctx->NewProjectionMatrix = GL_FALSE;
     break;
      case GL_TEXTURE:
     MEMCPY( ctx->TextureMatrix, Identity, 16*sizeof(GLfloat) );
         ctx->TextureMatrixType = MATRIX_IDENTITY;
     ctx->NewTextureMatrix = GL_FALSE;
     break;
      default:
         gl_problem(ctx, "Bad matrix mode in gl_LoadIdentity");
   }
}

Referenced by execute_list(), and init_exec_pointers().

gl_LoadMatrixf()

void gl_LoadMatrixf	(	GLcontext *	ctx,
		const GLfloat *	m
	)

Definition at line 738 of file matrix.c.

{
   if (INSIDE_BEGIN_END(ctx)) {
      gl_error( ctx,  GL_INVALID_OPERATION, "glLoadMatrix" );
      return;
   }
   switch (ctx->Transform.MatrixMode) {
      case GL_MODELVIEW:
         MEMCPY( ctx->ModelViewMatrix, m, 16*sizeof(GLfloat) );
     ctx->NewModelViewMatrix = GL_TRUE;
     break;
      case GL_PROJECTION:
     MEMCPY( ctx->ProjectionMatrix, m, 16*sizeof(GLfloat) );
     ctx->NewProjectionMatrix = GL_TRUE;
         {
            float n,f,c,d;
 
#define M(row,col)  m[col*4+row]
            c = M(2,2);
            d = M(2,3);
#undef M
            n = d / (c-1);
            f = d / (c+1);
 
            /* Need to keep a stack of near/far values in case the user
             * push/pops the projection matrix stack so that we can call
             * Driver.NearFar() after a pop.
             */
            ctx->NearFarStack[ctx->ProjectionStackDepth][0] = n;
            ctx->NearFarStack[ctx->ProjectionStackDepth][1] = f;
 
            if (ctx->Driver.NearFar) {
               (*ctx->Driver.NearFar)( ctx, n, f );
            }
         }
     break;
      case GL_TEXTURE:
     MEMCPY( ctx->TextureMatrix, m, 16*sizeof(GLfloat) );
     ctx->NewTextureMatrix = GL_TRUE;
     break;
      default:
         gl_problem(ctx, "Bad matrix mode in gl_LoadMatrixf");
   }
}

Referenced by execute_list(), and init_exec_pointers().

gl_MatrixMode()

void gl_MatrixMode	(	GLcontext *	ctx,
		GLenum	mode
	)

Definition at line 584 of file matrix.c.

{
   if (INSIDE_BEGIN_END(ctx)) {
      gl_error( ctx,  GL_INVALID_OPERATION, "glMatrixMode" );
      return;
   }
   switch (mode) {
      case GL_MODELVIEW:
      case GL_PROJECTION:
      case GL_TEXTURE:
         ctx->Transform.MatrixMode = mode;
         break;
      default:
         gl_error( ctx,  GL_INVALID_ENUM, "glMatrixMode" );
   }
}

Referenced by execute_list(), and init_exec_pointers().

gl_MultMatrixf()

void gl_MultMatrixf	(	GLcontext *	ctx,
		const GLfloat *	m
	)

Definition at line 785 of file matrix.c.

{
   if (INSIDE_BEGIN_END(ctx)) {
      gl_error( ctx,  GL_INVALID_OPERATION, "glMultMatrix" );
      return;
   }
   switch (ctx->Transform.MatrixMode) {
      case GL_MODELVIEW:
         matmul( ctx->ModelViewMatrix, ctx->ModelViewMatrix, m );
     ctx->NewModelViewMatrix = GL_TRUE;
     break;
      case GL_PROJECTION:
     matmul( ctx->ProjectionMatrix, ctx->ProjectionMatrix, m );
     ctx->NewProjectionMatrix = GL_TRUE;
     break;
      case GL_TEXTURE:
     matmul( ctx->TextureMatrix, ctx->TextureMatrix, m );
     ctx->NewTextureMatrix = GL_TRUE;
     break;
      default:
         gl_problem(ctx, "Bad matrix mode in gl_MultMatrixf");
   }
}

Referenced by execute_list(), gl_Frustum(), gl_Ortho(), gl_Rotatef(), and init_exec_pointers().

gl_Ortho()

void gl_Ortho	(	GLcontext *	ctx,
		GLdouble	left,
		GLdouble	right,
		GLdouble	bottom,
		GLdouble	top,
		GLdouble	nearval,
		GLdouble	farval
	)

Definition at line 553 of file matrix.c.

{
   GLfloat x, y, z;
   GLfloat tx, ty, tz;
   GLfloat m[16];
 
   x = 2.0 / (right-left);
   y = 2.0 / (top-bottom);
   z = -2.0 / (farval-nearval);
   tx = -(right+left) / (right-left);
   ty = -(top+bottom) / (top-bottom);
   tz = -(farval+nearval) / (farval-nearval);
 
#define M(row,col)  m[col*4+row]
   M(0,0) = x;     M(0,1) = 0.0F;  M(0,2) = 0.0F;  M(0,3) = tx;
   M(1,0) = 0.0F;  M(1,1) = y;     M(1,2) = 0.0F;  M(1,3) = ty;
   M(2,0) = 0.0F;  M(2,1) = 0.0F;  M(2,2) = z;     M(2,3) = tz;
   M(3,0) = 0.0F;  M(3,1) = 0.0F;  M(3,2) = 0.0F;  M(3,3) = 1.0F;
#undef M
 
   gl_MultMatrixf( ctx, m );
 
   if (ctx->Driver.NearFar) {
      (*ctx->Driver.NearFar)( ctx, nearval, farval );
   }
}

Referenced by execute_list(), and init_exec_pointers().

gl_PopMatrix()

void gl_PopMatrix

(

GLcontext *

ctx

)

Definition at line 653 of file matrix.c.

{
   if (INSIDE_BEGIN_END(ctx)) {
      gl_error( ctx,  GL_INVALID_OPERATION, "glPopMatrix" );
      return;
   }
   switch (ctx->Transform.MatrixMode) {
      case GL_MODELVIEW:
         if (ctx->ModelViewStackDepth==0) {
            gl_error( ctx,  GL_STACK_UNDERFLOW, "glPopMatrix");
            return;
         }
         ctx->ModelViewStackDepth--;
         MEMCPY( ctx->ModelViewMatrix,
                 ctx->ModelViewStack[ctx->ModelViewStackDepth],
                 16*sizeof(GLfloat) );
         ctx->NewModelViewMatrix = GL_TRUE;
         break;
      case GL_PROJECTION:
         if (ctx->ProjectionStackDepth==0) {
            gl_error( ctx,  GL_STACK_UNDERFLOW, "glPopMatrix");
            return;
         }
         ctx->ProjectionStackDepth--;
         MEMCPY( ctx->ProjectionMatrix,
                 ctx->ProjectionStack[ctx->ProjectionStackDepth],
                 16*sizeof(GLfloat) );
         ctx->NewProjectionMatrix = GL_TRUE;
 
         /* Device driver near/far values */
         {
            GLfloat nearVal = ctx->NearFarStack[ctx->ProjectionStackDepth][0];
            GLfloat farVal  = ctx->NearFarStack[ctx->ProjectionStackDepth][1];
            if (ctx->Driver.NearFar) {
               (*ctx->Driver.NearFar)( ctx, nearVal, farVal );
            }
         }
         break;
      case GL_TEXTURE:
         if (ctx->TextureStackDepth==0) {
            gl_error( ctx,  GL_STACK_UNDERFLOW, "glPopMatrix");
            return;
         }
         ctx->TextureStackDepth--;
         MEMCPY( ctx->TextureMatrix,
                 ctx->TextureStack[ctx->TextureStackDepth],
                 16*sizeof(GLfloat) );
         ctx->NewTextureMatrix = GL_TRUE;
         break;
      default:
         gl_problem(ctx, "Bad matrix mode in gl_PopMatrix");
   }
}

Referenced by execute_list(), and init_exec_pointers().

gl_PushMatrix()

void gl_PushMatrix

(

GLcontext *

ctx

)

Definition at line 603 of file matrix.c.

{
   if (INSIDE_BEGIN_END(ctx)) {
      gl_error( ctx,  GL_INVALID_OPERATION, "glPushMatrix" );
      return;
   }
   switch (ctx->Transform.MatrixMode) {
      case GL_MODELVIEW:
         if (ctx->ModelViewStackDepth>=MAX_MODELVIEW_STACK_DEPTH-1) {
            gl_error( ctx,  GL_STACK_OVERFLOW, "glPushMatrix");
            return;
         }
         MEMCPY( ctx->ModelViewStack[ctx->ModelViewStackDepth],
                 ctx->ModelViewMatrix,
                 16*sizeof(GLfloat) );
         ctx->ModelViewStackDepth++;
         break;
      case GL_PROJECTION:
         if (ctx->ProjectionStackDepth>=MAX_PROJECTION_STACK_DEPTH) {
            gl_error( ctx,  GL_STACK_OVERFLOW, "glPushMatrix");
            return;
         }
         MEMCPY( ctx->ProjectionStack[ctx->ProjectionStackDepth],
                 ctx->ProjectionMatrix,
                 16*sizeof(GLfloat) );
         ctx->ProjectionStackDepth++;
 
         /* Save near and far projection values */
         ctx->NearFarStack[ctx->ProjectionStackDepth][0]
            = ctx->NearFarStack[ctx->ProjectionStackDepth-1][0];
         ctx->NearFarStack[ctx->ProjectionStackDepth][1]
            = ctx->NearFarStack[ctx->ProjectionStackDepth-1][1];
         break;
      case GL_TEXTURE:
         if (ctx->TextureStackDepth>=MAX_TEXTURE_STACK_DEPTH) {
            gl_error( ctx,  GL_STACK_OVERFLOW, "glPushMatrix");
            return;
         }
         MEMCPY( ctx->TextureStack[ctx->TextureStackDepth],
                 ctx->TextureMatrix,
                 16*sizeof(GLfloat) );
         ctx->TextureStackDepth++;
         break;
      default:
         gl_problem(ctx, "Bad matrix mode in gl_PushMatrix");
   }
}

Referenced by execute_list(), and init_exec_pointers().

gl_Rotatef()

void gl_Rotatef	(	GLcontext *	ctx,
		GLfloat	angle,
		GLfloat	x,
		GLfloat	y,
		GLfloat	z
	)

Definition at line 927 of file matrix.c.

{
   GLfloat m[16];
   gl_rotation_matrix( angle, x, y, z, m );
   gl_MultMatrixf( ctx, m );
}

Referenced by init_exec_pointers().

gl_rotation_matrix()

void gl_rotation_matrix	(	GLfloat	angle,
		GLfloat	x,
		GLfloat	y,
		GLfloat	z,
		GLfloat	m[]
	)

Definition at line 814 of file matrix.c.

{
   /* This function contributed by Erich Boleyn (erich@uruk.org) */
   GLfloat mag, s, c;
   GLfloat xx, yy, zz, xy, yz, zx, xs, ys, zs, one_c;
 
   s = sin( angle * DEG2RAD );
   c = cos( angle * DEG2RAD );
 
   mag = GL_SQRT( x*x + y*y + z*z );
 
   if (mag == 0.0) {
      /* generate an identity matrix and return */
      MEMCPY(m, Identity, sizeof(GLfloat)*16);
      return;
   }
 
   x /= mag;
   y /= mag;
   z /= mag;
 
#define M(row,col)  m[col*4+row]
 
   /*
    *     Arbitrary axis rotation matrix.
    *
    *  This is composed of 5 matrices, Rz, Ry, T, Ry', Rz', multiplied
    *  like so:  Rz * Ry * T * Ry' * Rz'.  T is the final rotation
    *  (which is about the X-axis), and the two composite transforms
    *  Ry' * Rz' and Rz * Ry are (respectively) the rotations necessary
    *  from the arbitrary axis to the X-axis then back.  They are
    *  all elementary rotations.
    *
    *  Rz' is a rotation about the Z-axis, to bring the axis vector
    *  into the x-z plane.  Then Ry' is applied, rotating about the
    *  Y-axis to bring the axis vector parallel with the X-axis.  The
    *  rotation about the X-axis is then performed.  Ry and Rz are
    *  simply the respective inverse transforms to bring the arbitrary
    *  axis back to it's original orientation.  The first transforms
    *  Rz' and Ry' are considered inverses, since the data from the
    *  arbitrary axis gives you info on how to get to it, not how
    *  to get away from it, and an inverse must be applied.
    *
    *  The basic calculation used is to recognize that the arbitrary
    *  axis vector (x, y, z), since it is of unit length, actually
    *  represents the sines and cosines of the angles to rotate the
    *  X-axis to the same orientation, with theta being the angle about
    *  Z and phi the angle about Y (in the order described above)
    *  as follows:
    *
    *  cos ( theta ) = x / sqrt ( 1 - z^2 )
    *  sin ( theta ) = y / sqrt ( 1 - z^2 )
    *
    *  cos ( phi ) = sqrt ( 1 - z^2 )
    *  sin ( phi ) = z
    *
    *  Note that cos ( phi ) can further be inserted to the above
    *  formulas:
    *
    *  cos ( theta ) = x / cos ( phi )
    *  sin ( theta ) = y / sin ( phi )
    *
    *  ...etc.  Because of those relations and the standard trigonometric
    *  relations, it is pssible to reduce the transforms down to what
    *  is used below.  It may be that any primary axis chosen will give the
    *  same results (modulo a sign convention) using thie method.
    *
    *  Particularly nice is to notice that all divisions that might
    *  have caused trouble when parallel to certain planes or
    *  axis go away with care paid to reducing the expressions.
    *  After checking, it does perform correctly under all cases, since
    *  in all the cases of division where the denominator would have
    *  been zero, the numerator would have been zero as well, giving
    *  the expected result.
    */
 
   xx = x * x;
   yy = y * y;
   zz = z * z;
   xy = x * y;
   yz = y * z;
   zx = z * x;
   xs = x * s;
   ys = y * s;
   zs = z * s;
   one_c = 1.0F - c;
 
   M(0,0) = (one_c * xx) + c;
   M(0,1) = (one_c * xy) - zs;
   M(0,2) = (one_c * zx) + ys;
   M(0,3) = 0.0F;
 
   M(1,0) = (one_c * xy) + zs;
   M(1,1) = (one_c * yy) + c;
   M(1,2) = (one_c * yz) - xs;
   M(1,3) = 0.0F;
 
   M(2,0) = (one_c * zx) - ys;
   M(2,1) = (one_c * yz) + xs;
   M(2,2) = (one_c * zz) + c;
   M(2,3) = 0.0F;
 
   M(3,0) = 0.0F;
   M(3,1) = 0.0F;
   M(3,2) = 0.0F;
   M(3,3) = 1.0F;
 
#undef M
}

Referenced by gl_Rotatef(), and gl_save_Rotatef().

gl_Scalef()

void gl_Scalef	(	GLcontext *	ctx,
		GLfloat	x,
		GLfloat	y,
		GLfloat	z
	)

Definition at line 940 of file matrix.c.

{
   GLfloat *m;
 
   if (INSIDE_BEGIN_END(ctx)) {
      gl_error( ctx,  GL_INVALID_OPERATION, "glScale" );
      return;
   }
   switch (ctx->Transform.MatrixMode) {
      case GL_MODELVIEW:
         m = ctx->ModelViewMatrix;
     ctx->NewModelViewMatrix = GL_TRUE;
     break;
      case GL_PROJECTION:
         m = ctx->ProjectionMatrix;
     ctx->NewProjectionMatrix = GL_TRUE;
     break;
      case GL_TEXTURE:
         m = ctx->TextureMatrix;
     ctx->NewTextureMatrix = GL_TRUE;
     break;
      default:
         gl_problem(ctx, "Bad matrix mode in gl_Scalef");
         return;
   }
   m[0] *= x;   m[4] *= y;   m[8]  *= z;
   m[1] *= x;   m[5] *= y;   m[9]  *= z;
   m[2] *= x;   m[6] *= y;   m[10] *= z;
   m[3] *= x;   m[7] *= y;   m[11] *= z;
}

Referenced by execute_list(), and init_exec_pointers().

gl_Translatef()

void gl_Translatef	(	GLcontext *	ctx,
		GLfloat	x,
		GLfloat	y,
		GLfloat	z
	)

Definition at line 976 of file matrix.c.

{
   GLfloat *m;
   if (INSIDE_BEGIN_END(ctx)) {
      gl_error( ctx, GL_INVALID_OPERATION, "glTranslate" );
      return;
   }
   switch (ctx->Transform.MatrixMode) {
      case GL_MODELVIEW:
         m = ctx->ModelViewMatrix;
     ctx->NewModelViewMatrix = GL_TRUE;
     break;
      case GL_PROJECTION:
         m = ctx->ProjectionMatrix;
     ctx->NewProjectionMatrix = GL_TRUE;
     break;
      case GL_TEXTURE:
         m = ctx->TextureMatrix;
     ctx->NewTextureMatrix = GL_TRUE;
     break;
      default:
         gl_problem(ctx, "Bad matrix mode in gl_Translatef");
         return;
   }
 
   m[12] = m[0] * x + m[4] * y + m[8]  * z + m[12];
   m[13] = m[1] * x + m[5] * y + m[9]  * z + m[13];
   m[14] = m[2] * x + m[6] * y + m[10] * z + m[14];
   m[15] = m[3] * x + m[7] * y + m[11] * z + m[15];
}

Referenced by execute_list(), and init_exec_pointers().

gl_Viewport()

void gl_Viewport	(	GLcontext *	ctx,
		GLint	x,
		GLint	y,
		GLsizei	width,
		GLsizei	height
	)

Definition at line 1014 of file matrix.c.

{
   if (width<0 || height<0) {
      gl_error( ctx,  GL_INVALID_VALUE, "glViewport" );
      return;
   }
   if (INSIDE_BEGIN_END(ctx)) {
      gl_error( ctx,  GL_INVALID_OPERATION, "glViewport" );
      return;
   }
 
   /* clamp width, and height to implementation dependent range */
   width  = CLAMP( width,  1, MAX_WIDTH );
   height = CLAMP( height, 1, MAX_HEIGHT );
 
   /* Save viewport */
   ctx->Viewport.X = x;
   ctx->Viewport.Width = width;
   ctx->Viewport.Y = y;
   ctx->Viewport.Height = height;
 
   /* compute scale and bias values */
   ctx->Viewport.Sx = (GLfloat) width / 2.0F;
   ctx->Viewport.Tx = ctx->Viewport.Sx + x;
   ctx->Viewport.Sy = (GLfloat) height / 2.0F;
   ctx->Viewport.Ty = ctx->Viewport.Sy + y;
 
   ctx->NewState |= NEW_ALL;   /* just to be safe */
 
   /* Check if window/buffer has been resized and if so, reallocate the
    * ancillary buffers.
    */
   gl_ResizeBuffersMESA(ctx);
}

Referenced by execute_list(), init_exec_pointers(), and sw_SetContext().

invert_matrix()

static void invert_matrix ( const GLfloat *  m, GLfloat *  out  )

static

Definition at line 290 of file matrix.c.

{
/* NB. OpenGL Matrices are COLUMN major. */
#define MAT(m,r,c) (m)[(c)*4+(r)]
 
/* Here's some shorthand converting standard (row,column) to index. */
#define m11 MAT(m,0,0)
#define m12 MAT(m,0,1)
#define m13 MAT(m,0,2)
#define m14 MAT(m,0,3)
#define m21 MAT(m,1,0)
#define m22 MAT(m,1,1)
#define m23 MAT(m,1,2)
#define m24 MAT(m,1,3)
#define m31 MAT(m,2,0)
#define m32 MAT(m,2,1)
#define m33 MAT(m,2,2)
#define m34 MAT(m,2,3)
#define m41 MAT(m,3,0)
#define m42 MAT(m,3,1)
#define m43 MAT(m,3,2)
#define m44 MAT(m,3,3)
 
   register GLfloat det;
   GLfloat tmp[16]; /* Allow out == in. */
 
   if( m41 != 0. || m42 != 0. || m43 != 0. || m44 != 1. ) {
      invert_matrix_general(m, out);
      return;
   }
 
   /* Inverse = adjoint / det. (See linear algebra texts.)*/
 
   tmp[0]= m22 * m33 - m23 * m32;
   tmp[1]= m23 * m31 - m21 * m33;
   tmp[2]= m21 * m32 - m22 * m31;
 
   /* Compute determinant as early as possible using these cofactors. */
   det= m11 * tmp[0] + m12 * tmp[1] + m13 * tmp[2];
 
   /* Run singularity test. */
   if (det == 0.0F) {
      /* printf("invert_matrix: Warning: Singular matrix.\n"); */
      MEMCPY( out, Identity, 16*sizeof(GLfloat) );
   }
   else {
      GLfloat d12, d13, d23, d24, d34, d41;
      register GLfloat im11, im12, im13, im14;
 
      det= 1. / det;
 
      /* Compute rest of inverse. */
      tmp[0] *= det;
      tmp[1] *= det;
      tmp[2] *= det;
      tmp[3]  = 0.;
 
      im11= m11 * det;
      im12= m12 * det;
      im13= m13 * det;
      im14= m14 * det;
      tmp[4] = im13 * m32 - im12 * m33;
      tmp[5] = im11 * m33 - im13 * m31;
      tmp[6] = im12 * m31 - im11 * m32;
      tmp[7] = 0.;
 
      /* Pre-compute 2x2 dets for first two rows when computing */
      /* cofactors of last two rows. */
      d12 = im11*m22 - m21*im12;
      d13 = im11*m23 - m21*im13;
      d23 = im12*m23 - m22*im13;
      d24 = im12*m24 - m22*im14;
      d34 = im13*m24 - m23*im14;
      d41 = im14*m21 - m24*im11;
 
      tmp[8] =  d23;
      tmp[9] = -d13;
      tmp[10] = d12;
      tmp[11] = 0.;
 
      tmp[12] = -(m32 * d34 - m33 * d24 + m34 * d23);
      tmp[13] =  (m31 * d34 + m33 * d41 + m34 * d13);
      tmp[14] = -(m31 * d24 + m32 * d41 + m34 * d12);
      tmp[15] =  1.;
 
      MEMCPY(out, tmp, 16*sizeof(GLfloat));
  }
 
#undef m11
#undef m12
#undef m13
#undef m14
#undef m21
#undef m22
#undef m23
#undef m24
#undef m31
#undef m32
#undef m33
#undef m34
#undef m41
#undef m42
#undef m43
#undef m44
#undef MAT
}

Referenced by gl_analyze_modelview_matrix().

invert_matrix_general()

static void invert_matrix_general ( const GLfloat *  m, GLfloat *  out  )

static

Definition at line 199 of file matrix.c.

{
   Mat2 r1, r2, r3, r4, r5, r6, r7;
   const GLfloat * A = m;
   GLfloat *       C = out;
   GLfloat one_over_det;
 
   /*
    * A is the 4x4 source matrix (to be inverted).
    * C is the 4x4 destination matrix
    * a11 is the 2x2 matrix in the upper left quadrant of A
    * a12 is the 2x2 matrix in the upper right quadrant of A
    * a21 is the 2x2 matrix in the lower left quadrant of A
    * a22 is the 2x2 matrix in the lower right quadrant of A
    * similarly, cXX are the 2x2 quadrants of the destination matrix
    */
 
   /* R1 = inverse( a11 ) */
   one_over_det = 1.0f / ( ( A[M00] * A[M11] ) - ( A[M10] * A[M01] ) );
   r1[0][0] = one_over_det * A[M11];
   r1[0][1] = one_over_det * -A[M01];
   r1[1][0] = one_over_det * -A[M10];
   r1[1][1] = one_over_det * A[M00];
 
   /* R2 = a21 x R1 */
   r2[0][0] = A[M20] * r1[0][0] + A[M21] * r1[1][0];
   r2[0][1] = A[M20] * r1[0][1] + A[M21] * r1[1][1];
   r2[1][0] = A[M30] * r1[0][0] + A[M31] * r1[1][0];
   r2[1][1] = A[M30] * r1[0][1] + A[M31] * r1[1][1];
 
   /* R3 = R1 x a12 */
   r3[0][0] = r1[0][0] * A[M02] + r1[0][1] * A[M12];
   r3[0][1] = r1[0][0] * A[M03] + r1[0][1] * A[M13];
   r3[1][0] = r1[1][0] * A[M02] + r1[1][1] * A[M12];
   r3[1][1] = r1[1][0] * A[M03] + r1[1][1] * A[M13];
 
   /* R4 = a21 x R3 */
   r4[0][0] = A[M20] * r3[0][0] + A[M21] * r3[1][0];
   r4[0][1] = A[M20] * r3[0][1] + A[M21] * r3[1][1];
   r4[1][0] = A[M30] * r3[0][0] + A[M31] * r3[1][0];
   r4[1][1] = A[M30] * r3[0][1] + A[M31] * r3[1][1];
 
   /* R5 = R4 - a22 */
   r5[0][0] = r4[0][0] - A[M22];
   r5[0][1] = r4[0][1] - A[M23];
   r5[1][0] = r4[1][0] - A[M32];
   r5[1][1] = r4[1][1] - A[M33];
 
   /* R6 = inverse( R5 ) */
   one_over_det = 1.0f / ( ( r5[0][0] * r5[1][1] ) - ( r5[1][0] * r5[0][1] ) );
   r6[0][0] = one_over_det * r5[1][1];
   r6[0][1] = one_over_det * -r5[0][1];
   r6[1][0] = one_over_det * -r5[1][0];
   r6[1][1] = one_over_det * r5[0][0];
 
   /* c12 = R3 x R6 */
   C[M02] = r3[0][0] * r6[0][0] + r3[0][1] * r6[1][0];
   C[M03] = r3[0][0] * r6[0][1] + r3[0][1] * r6[1][1];
   C[M12] = r3[1][0] * r6[0][0] + r3[1][1] * r6[1][0];
   C[M13] = r3[1][0] * r6[0][1] + r3[1][1] * r6[1][1];
 
   /* c21 = R6 x R2 */
   C[M20] = r6[0][0] * r2[0][0] + r6[0][1] * r2[1][0];
   C[M21] = r6[0][0] * r2[0][1] + r6[0][1] * r2[1][1];
   C[M30] = r6[1][0] * r2[0][0] + r6[1][1] * r2[1][0];
   C[M31] = r6[1][0] * r2[0][1] + r6[1][1] * r2[1][1];
 
   /* R7 = R3 x c21 */
   r7[0][0] = r3[0][0] * C[M20] + r3[0][1] * C[M30];
   r7[0][1] = r3[0][0] * C[M21] + r3[0][1] * C[M31];
   r7[1][0] = r3[1][0] * C[M20] + r3[1][1] * C[M30];
   r7[1][1] = r3[1][0] * C[M21] + r3[1][1] * C[M31];
 
   /* c11 = R1 - R7 */
   C[M00] = r1[0][0] - r7[0][0];
   C[M01] = r1[0][1] - r7[0][1];
   C[M10] = r1[1][0] - r7[1][0];
   C[M11] = r1[1][1] - r7[1][1];
 
   /* c22 = -R6 */
   C[M22] = -r6[0][0];
   C[M23] = -r6[0][1];
   C[M32] = -r6[1][0];
   C[M33] = -r6[1][1];
}

Referenced by invert_matrix().

is_identity()

static GLboolean is_identity ( const GLfloat  m[16] )

static

Definition at line 402 of file matrix.c.

{
   if (   m[0]==1.0F && m[4]==0.0F && m[ 8]==0.0F && m[12]==0.0F
       && m[1]==0.0F && m[5]==1.0F && m[ 9]==0.0F && m[13]==0.0F
       && m[2]==0.0F && m[6]==0.0F && m[10]==1.0F && m[14]==0.0F
       && m[3]==0.0F && m[7]==0.0F && m[11]==0.0F && m[15]==1.0F) {
      return GL_TRUE;
   }
   else {
      return GL_FALSE;
   }
}

Referenced by brush_fill_pixels(), gl_analyze_modelview_matrix(), gl_analyze_projection_matrix(), and gl_analyze_texture_matrix().

matmul()

static void matmul ( GLfloat *  product, const GLfloat *  a, const GLfloat *  b  )

static

Definition at line 154 of file matrix.c.

{
   /* This matmul was contributed by Thomas Malik */
   GLint i;
 
#define A(row,col)  a[(col<<2)+row]
#define B(row,col)  b[(col<<2)+row]
#define P(row,col)  product[(col<<2)+row]
 
   /* i-te Zeile */
   for (i = 0; i < 4; i++) {
      GLfloat ai0=A(i,0),  ai1=A(i,1),  ai2=A(i,2),  ai3=A(i,3);
      P(i,0) = ai0 * B(0,0) + ai1 * B(1,0) + ai2 * B(2,0) + ai3 * B(3,0);
      P(i,1) = ai0 * B(0,1) + ai1 * B(1,1) + ai2 * B(2,1) + ai3 * B(3,1);
      P(i,2) = ai0 * B(0,2) + ai1 * B(1,2) + ai2 * B(2,2) + ai3 * B(3,2);
      P(i,3) = ai0 * B(0,3) + ai1 * B(1,3) + ai2 * B(2,3) + ai3 * B(3,3);
   }
 
#undef A
#undef B
#undef P
}

Referenced by gl_MultMatrixf().

Variable Documentation

Identity

GLfloat Identity[16]

static

Initial value:

= {
   1.0, 0.0, 0.0, 0.0,
   0.0, 1.0, 0.0, 0.0,
   0.0, 0.0, 1.0, 0.0,
   0.0, 0.0, 0.0, 1.0
}

Definition at line 127 of file matrix.c.

Referenced by gl_LoadIdentity(), gl_rotation_matrix(), and invert_matrix().