monoChain.cc File Reference

#include "gluos.h"
#include "zlassert.h"
#include "monoChain.h"
#include "quicksort.h"
#include "searchTree.h"
#include "polyUtil.h"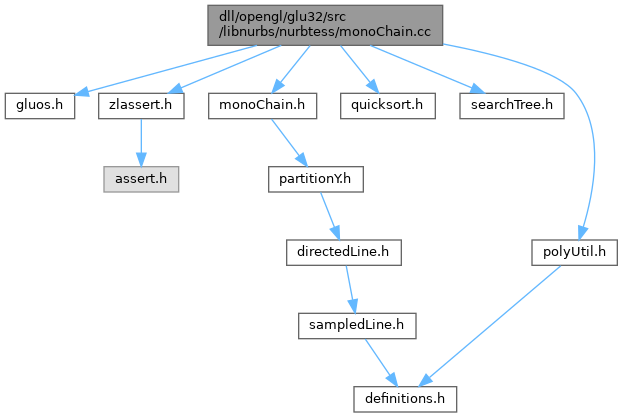

Include dependency graph for monoChain.cc:

Go to the source code of this file.

Macros
#define	max(a, b)   ((a>b)? a:b)
#define	min(a, b)   ((a>b)? b:a)

Functions
Int	isCusp (directedLine *v)
Int	deleteRepeatDiagonals (Int num_diagonals, directedLine **diagonal_vertices, directedLine **new_vertices)
Real	intersectHoriz (Real x1, Real y1, Real x2, Real y2, Real y)
static int	compChainHeadInY (monoChain *mc1, monoChain *mc2)
monoChain *	directedLineLoopToMonoChainLoop (directedLine *loop)
monoChain *	directedLineLoopListToMonoChainLoopList (directedLine *list)
static Int	compEdges (directedLine *e1, directedLine *e2)
Int	compChains (monoChain *mc1, monoChain *mc2)
Int	MC_sweepY (Int nVertices, monoChain **sortedVertices, sweepRange **ret_ranges)
void	MC_findDiagonals (Int total_num_edges, monoChain **sortedVertices, sweepRange **ranges, Int &num_diagonals, directedLine **diagonal_vertices)
directedLine *	MC_partitionY (directedLine *polygons, sampledLine **retSampledLines)

Macro Definition Documentation

max

#define max	(		a,
			b
	)		((a>b)? a:b)

Definition at line 52 of file monoChain.cc.

min

#define min	(		a,
			b
	)		((a>b)? b:a)

Examples

/srv/doxygen/reactos/win32ss/gdi/gdi32/objects/utils.c.

Definition at line 55 of file monoChain.cc.

Function Documentation

compChainHeadInY()

static int compChainHeadInY ( monoChain *  mc1, monoChain *  mc2  )

static

Definition at line 85 of file monoChain.cc.

{
  return compV2InY(mc1->getHead()->head(), mc2->getHead()->head());
}

Referenced by MC_partitionY().

compChains()

Int compChains	(	monoChain *	mc1,
		monoChain *	mc2
	)

Definition at line 376 of file monoChain.cc.

{
  Real y;
  assert(mc1->isKey || mc2->isKey);
  if(mc1->isKey)
    y = mc1->keyY;
  else
    y = mc2->keyY;
  directedLine *d1 = mc1->find(y);
  directedLine *d2 = mc2->find(y);
  mc2->find(y);
//  Real x1 = mc1->chainIntersectHoriz(y);
//  Real x2 = mc2->chainIntersectHoriz(y);
  return   compEdges(d1, d2);
}

Referenced by MC_sweepY().

compEdges()

static Int compEdges ( directedLine *  e1, directedLine *  e2  )

static

Definition at line 296 of file monoChain.cc.

{
  Real* head1 = e1->head();
  Real* tail1 = e1->tail();
  Real* head2 = e2->head();
  Real* tail2 = e2->tail();
/*
  Real h10 = head1[0];
  Real h11 = head1[1];
  Real t10 = tail1[0];
  Real t11 = tail1[1];
  Real h20 = head2[0];
  Real h21 = head2[1];
  Real t20 = tail2[0];
  Real t21 = tail2[1];
*/
  Real e1_Ymax, e1_Ymin, e2_Ymax, e2_Ymin;
/*
  if(h11>t11) {
    e1_Ymax= h11;
    e1_Ymin= t11;
  }
  else{
    e1_Ymax = t11;
    e1_Ymin = h11;
  }
 
  if(h21>t21) {
    e2_Ymax= h21;
    e2_Ymin= t21;
  }
  else{
    e2_Ymax = t21;
    e2_Ymin = h21;
  }
*/
 
  if(head1[1]>tail1[1]) {
    e1_Ymax= head1[1];
    e1_Ymin= tail1[1];
  }
  else{
    e1_Ymax = tail1[1];
    e1_Ymin = head1[1];
  }
 
  if(head2[1]>tail2[1]) {
    e2_Ymax= head2[1];
    e2_Ymin= tail2[1];
  }
  else{
    e2_Ymax = tail2[1];
    e2_Ymin = head2[1];
  }
 
  
  /*Real e1_Ymax = max(head1[1], tail1[1]);*/ /*max(e1->head()[1], e1->tail()[1]);*/
  /*Real e1_Ymin = min(head1[1], tail1[1]);*/ /*min(e1->head()[1], e1->tail()[1]);*/
  /*Real e2_Ymax = max(head2[1], tail2[1]);*/ /*max(e2->head()[1], e2->tail()[1]);*/
  /*Real e2_Ymin = min(head2[1], tail2[1]);*/ /*min(e2->head()[1], e2->tail()[1]);*/
 
  Real Ymax = min(e1_Ymax, e2_Ymax);
  Real Ymin = max(e1_Ymin, e2_Ymin);
    
  Real y = 0.5*(Ymax + Ymin);
 
/*  Real x1 = intersectHoriz(e1->head()[0], e1->head()[1], e1->tail()[0], e1->tail()[1], y);
  Real x2 = intersectHoriz(e2->head()[0], e2->head()[1], e2->tail()[0], e2->tail()[1], y);
*/
/*
  Real x1 = intersectHoriz(h10, h11, t10, t11, y);
  Real x2 = intersectHoriz(h20, h21, t20, t21, y);
*/
  Real x1 = intersectHoriz(head1[0], head1[1], tail1[0], tail1[1], y);
  Real x2 = intersectHoriz(head2[0], head2[1], tail2[0], tail2[1], y);
 
  if(x1<= x2) return -1;
  else return 1;
}

Referenced by compChains(), and MC_findDiagonals().

deleteRepeatDiagonals()

Int deleteRepeatDiagonals	(	Int	num_diagonals,
		directedLine **	diagonal_vertices,
		directedLine **	new_vertices
	)

Definition at line 386 of file partitionY.cc.

{
  Int i,k;
  Int j,l;
  Int index;
  index=0;
  for(i=0,k=0; i<num_diagonals; i++, k+=2)
    {
      Int isRepeated=0;
      /*check the diagonla (diagonal_vertice[k], diagonal_vertices[k+1])
       *is repeated or not
       */
      for(j=0,l=0; j<index; j++, l+=2)
    {
      if(
         (diagonal_vertices[k] == new_vertices[l] && 
          diagonal_vertices[k+1] == new_vertices[l+1]
          )
         ||
         (
          diagonal_vertices[k] == new_vertices[l+1] && 
          diagonal_vertices[k+1] == new_vertices[l]
          )
         )
        {
          isRepeated=1;
          break;
        }
    }
      if(! isRepeated)
    {
      new_vertices[index+index] = diagonal_vertices[k];
      new_vertices[index+index+1] = diagonal_vertices[k+1];   
      index++;
    }
    }
  return index;
}

Referenced by DBGfindDiagonals(), MC_partitionY(), and partitionY().

directedLineLoopListToMonoChainLoopList()

monoChain * directedLineLoopListToMonoChainLoopList

(

directedLine *

list

)

Definition at line 273 of file monoChain.cc.

{
  directedLine* temp;
  monoChain* mc;
  monoChain* mcEnd;
  mc = directedLineLoopToMonoChainLoop(list);
  mcEnd = mc;  
  for(temp = list->getNextPolygon(); temp != NULL; temp = temp->getNextPolygon())
    {
      monoChain *newLoop = directedLineLoopToMonoChainLoop(temp);
      mcEnd->setNextPolygon(newLoop);
      mcEnd = newLoop;
    }
  return mc;
}

Referenced by MC_partitionY().

directedLineLoopToMonoChainLoop()

monoChain * directedLineLoopToMonoChainLoop

(

directedLine *

loop

)

Definition at line 232 of file monoChain.cc.

{
  directedLine *temp;
  monoChain *ret=NULL;
 
  //find the first cusp
  directedLine *prevCusp=NULL;
  directedLine *firstCusp;
 
  if(isCusp(loop))
    prevCusp = loop;
  else
    {
      for(temp = loop->getNext(); temp != loop; temp = temp->getNext())
    if(isCusp(temp))
      break;
      prevCusp = temp;
    }
  firstCusp = prevCusp;
//printf("first cusp is (%f,%f), (%f,%f), (%f,%f)\n", prevCusp->getPrev()->head()[0], prevCusp->getPrev()->head()[1], prevCusp->head()[0], prevCusp->head()[1], prevCusp->tail()[0], prevCusp->tail()[1]);
 
  for(temp = prevCusp->getNext(); temp != loop; temp = temp->getNext())
    {
      if(isCusp(temp))
    {
//printf("the cusp is (%f,%f), (%f,%f), (%f,%f)\n", temp->getPrev()->head()[0], temp->getPrev()->head()[1], temp->head()[0], temp->head()[1], temp->tail()[0], temp->tail()[1]);
      if(ret == NULL)
        {
          ret = new monoChain(prevCusp, temp);
        }
      else
        ret->insert(new monoChain(prevCusp, temp));
      prevCusp = temp;    
    }
    }
  assert(ret);
  ret->insert(new monoChain(prevCusp, firstCusp));
 
  return ret;
}

Referenced by directedLineLoopListToMonoChainLoopList().

intersectHoriz()

Real intersectHoriz ( Real  x1, Real  y1, Real  x2, Real  y2, Real  y  )

inline

Definition at line 79 of file monoChain.cc.

{
  return ((y2==y1)? (x1+x2)*0.5 : x1 + ((y-y1)/(y2-y1)) * (x2-x1));
}

Referenced by monoChain::chainIntersectHoriz(), and compEdges().

isCusp()

Int isCusp

(

directedLine *

v

)

Definition at line 100 of file partitionY.cc.

{
  Real *A=v->getPrev()->head();
  Real *B=v->head();
  Real *C=v->tail();
  if(A[1] < B[1] && B[1] < C[1])
    return 0;
  else if(A[1] > B[1] && B[1] > C[1])
    return 0;
  else if(A[1] < B[1] && C[1] < B[1])
    return 1;
  else if(A[1] > B[1] && C[1] > B[1])
    return 1;
 
  if((isAbove(v, v) && isAbove(v, v->getPrev())) ||
     (isBelow(v, v) && isBelow(v, v->getPrev())))
    return 1;
  else
    return 0;
}

Referenced by cuspType(), and directedLineLoopToMonoChainLoop().

MC_findDiagonals()

void MC_findDiagonals	(	Int	total_num_edges,
		monoChain **	sortedVertices,
		sweepRange **	ranges,
		Int &	num_diagonals,
		directedLine **	diagonal_vertices
	)

Definition at line 567 of file monoChain.cc.

{
  Int i,j,k;
  k=0;
  //reset 'current' of all the monoChains
  for(i=0; i<total_num_edges; i++)
    sortedVertices[i]->resetCurrent();
  
  for(i=0; i<total_num_edges; i++)
    {
      directedLine* vert = sortedVertices[i]->getHead();
      directedLine* thisEdge = vert;
      directedLine* prevEdge = vert->getPrev();
      if(isBelow(vert, thisEdge) && isBelow(vert, prevEdge) && compEdges(prevEdge, thisEdge)<0)
    {
      //this is an upward interior cusp
      diagonal_vertices[k++] = vert;
 
      directedLine* leftEdge = ranges[i]->left;
      directedLine* rightEdge = ranges[i]->right;
      
      directedLine* leftVert = leftEdge;
      directedLine* rightVert = rightEdge->getNext();
      assert(leftVert->head()[1] >= vert->head()[1]);
      assert(rightVert->head()[1] >= vert->head()[1]);
      directedLine* minVert = (leftVert->head()[1] <= rightVert->head()[1])?leftVert:rightVert;
      Int found = 0;
      for(j=i+1; j<total_num_edges; j++)
        {
          if(sortedVertices[j]->getHead()->head()[1] > minVert->head()[1])
        break;
          
          if(sweepRangeEqual(ranges[i], ranges[j]))
        {
          found = 1;
          break;
        }
        }
 
      if(found)
        diagonal_vertices[k++] = sortedVertices[j]->getHead();
      else
        diagonal_vertices[k++] = minVert;
    }     
      else if(isAbove(vert, thisEdge) && isAbove(vert, prevEdge) && compEdges(prevEdge, thisEdge)>0)
    {
      //downward interior cusp
      diagonal_vertices[k++] = vert;
      directedLine* leftEdge = ranges[i]->left;
      directedLine* rightEdge = ranges[i]->right;
      directedLine* leftVert = leftEdge->getNext();
      directedLine* rightVert = rightEdge;
      assert(leftVert->head()[1] <= vert->head()[1]);
      assert(rightVert->head()[1] <= vert->head()[1]);
      directedLine* maxVert = (leftVert->head()[1] > rightVert->head()[1])? leftVert:rightVert;
      Int found=0;
      for(j=i-1; j>=0; j--)
        {
          if(sortedVertices[j]->getHead()->head()[1] < maxVert->head()[1])
        break;
          if(sweepRangeEqual(ranges[i], ranges[j]))
        {
          found = 1;
          break;
        }
        }
      if(found)
        diagonal_vertices[k++] = sortedVertices[j]->getHead();
      else
        diagonal_vertices[k++] = maxVert;
    }
    }
  num_diagonals = k/2;
}

Referenced by MC_partitionY().

MC_partitionY()

directedLine * MC_partitionY	(	directedLine *	polygons,
		sampledLine **	retSampledLines
	)

Definition at line 647 of file monoChain.cc.

{
//printf("enter mc_partitionY\n");
  Int total_num_chains = 0;
  monoChain* loopList = directedLineLoopListToMonoChainLoopList(polygons);
  monoChain** array = loopList->toArrayAllLoops(total_num_chains);
 
  if(total_num_chains<=2) //there is just one single monotone polygon
    {
      loopList->deleteLoopList();
      free(array); 
      *retSampledLines = NULL;
      return polygons;
    }
 
//loopList->printAllLoops();
//printf("total_num_chains=%i\n", total_num_chains);
  quicksort( (void**)array, 0, total_num_chains-1, (Int (*)(void*, void*))compChainHeadInY);
//printf("after quicksort\n");  
 
  sweepRange** ranges = (sweepRange**)malloc(sizeof(sweepRange*) * (total_num_chains));
  assert(ranges);
 
  if(MC_sweepY(total_num_chains, array, ranges))
    {
      loopList->deleteLoopList();
      free(array); 
      *retSampledLines = NULL;
      return NULL;
    }
//printf("after MC_sweepY\n");
 
 
  Int num_diagonals;
  /*number diagonals is < total_num_edges*total_num_edges*/
  directedLine** diagonal_vertices = (directedLine**) malloc(sizeof(directedLine*) * total_num_chains*2/*total_num_edges*/);
  assert(diagonal_vertices);
 
//printf("before call MC_findDiagonales\n");
 
  MC_findDiagonals(total_num_chains, array, ranges, num_diagonals, diagonal_vertices);
//printf("after call MC_findDia, num_diagnla=%i\n", num_diagonals);
 
  directedLine* ret_polygons = polygons;
  sampledLine* newSampledLines = NULL;
  Int i,k;
 
  num_diagonals=deleteRepeatDiagonals(num_diagonals, diagonal_vertices, diagonal_vertices);
 
 
 
//drawDiagonals(num_diagonals, diagonal_vertices);
//printf("diagoanls are \n");
//for(i=0; i<num_diagonals; i++)
//  {
//    printf("(%f,%f)\n", diagonal_vertices[2*i]->head()[0], diagonal_vertices[2*i]->head()[1]);
//    printf("**(%f,%f)\n", diagonal_vertices[2*i+1]->head()[0], diagonal_vertices[2*i+1]->head()[1]);
//  }
 
  Int *removedDiagonals=(Int*)malloc(sizeof(Int) * num_diagonals);
  for(i=0; i<num_diagonals; i++)
    removedDiagonals[i] = 0;
//  printf("first pass\n");
 
 
 for(i=0,k=0; i<num_diagonals; i++,k+=2)
    {
 
 
      directedLine* v1=diagonal_vertices[k];
      directedLine* v2=diagonal_vertices[k+1];
      directedLine* ret_p1;
      directedLine* ret_p2;
      
      /*we ahve to determine whether v1 and v2 belong to the same polygon before
       *their structure are modified by connectDiagonal().
       */
/*
      directedLine *root1 = v1->findRoot();
      directedLine *root2 = v2->findRoot();
      assert(root1);      
      assert(root2);
*/
 
directedLine*  root1 = v1->rootLinkFindRoot();
directedLine*  root2 = v2->rootLinkFindRoot();
 
      if(root1 != root2)
    {
 
      removedDiagonals[i] = 1;
      sampledLine* generatedLine;
 
 
 
      v1->connectDiagonal(v1,v2, &ret_p1, &ret_p2, &generatedLine, ret_polygons);
 
 
 
      newSampledLines = generatedLine->insert(newSampledLines);
/*
      ret_polygons = ret_polygons->cutoffPolygon(root1);
 
      ret_polygons = ret_polygons->cutoffPolygon(root2);
      ret_polygons = ret_p1->insertPolygon(ret_polygons);
root1->rootLinkSet(ret_p1);
root2->rootLinkSet(ret_p1);
ret_p1->rootLinkSet(NULL);
ret_p2->rootLinkSet(ret_p1);
*/
      ret_polygons = ret_polygons->cutoffPolygon(root2);
 
 
 
root2->rootLinkSet(root1);
ret_p1->rootLinkSet(root1);
ret_p2->rootLinkSet(root1);
 
       /*now that we have connected the diagonal v1 and v2, 
        *we have to check those unprocessed diagonals which 
        *have v1 or v2 as an end point. Notice that the head of v1
        *has the same coodinates as the head of v2->prev, and the head of
        *v2 has the same coordinate as the head of v1->prev. 
        *Suppose these is a diagonal (v1, x). If (v1,x) is still a valid
        *diagonal, then x should be on the left hand side of the directed line:        *v1->prev->head -- v1->head -- v1->tail. Otherwise, (v1,x) should be  
        *replaced by (v2->prev, x), that is, x is on the left of 
        * v2->prev->prev->head, v2->prev->head, v2->prev->tail.
        */
        Int ii, kk;
        for(ii=0, kk=0; ii<num_diagonals; ii++, kk+=2)
      if( removedDiagonals[ii]==0)
        {
          directedLine* d1=diagonal_vertices[kk];
          directedLine* d2=diagonal_vertices[kk+1];
          /*check d1, and replace diagonal_vertices[kk] if necessary*/
          if(d1 == v1) {
        /*check if d2 is to left of v1->prev->head:v1->head:v1->tail*/
        if(! pointLeft2Lines(v1->getPrev()->head(), 
                     v1->head(), v1->tail(), d2->head()))
          {
/*
            assert(pointLeft2Lines(v2->getPrev()->getPrev()->head(),
                       v2->getPrev()->head(), 
                       v2->getPrev()->tail(), d2->head()));
*/
            diagonal_vertices[kk] = v2->getPrev();
          }
          }
          if(d1 == v2) {
        /*check if d2 is to left of v2->prev->head:v2->head:v2->tail*/
        if(! pointLeft2Lines(v2->getPrev()->head(),
                     v2->head(), v2->tail(), d2->head()))
          {
/*
            assert(pointLeft2Lines(v1->getPrev()->getPrev()->head(),
                       v1->getPrev()->head(),
                       v1->getPrev()->tail(), d2->head()));
*/
            diagonal_vertices[kk] = v1->getPrev();
          }
          }
          /*check d2 and replace diagonal_vertices[k+1] if necessary*/
          if(d2 == v1) {
        /*check if d1 is to left of v1->prev->head:v1->head:v1->tail*/
        if(! pointLeft2Lines(v1->getPrev()->head(), 
                     v1->head(), v1->tail(), d1->head()))
          {
/*          assert(pointLeft2Lines(v2->getPrev()->getPrev()->head(),
                       v2->getPrev()->head(), 
                       v2->getPrev()->tail(), d1->head()));
*/
            diagonal_vertices[kk+1] = v2->getPrev();
          }
          }
          if(d2 == v2) {
        /*check if d1 is to left of v2->prev->head:v2->head:v2->tail*/
        if(! pointLeft2Lines(v2->getPrev()->head(),
                     v2->head(), v2->tail(), d1->head()))
          {
/*          assert(pointLeft2Lines(v1->getPrev()->getPrev()->head(),
                       v1->getPrev()->head(),
                       v1->getPrev()->tail(), d1->head()));
*/
            diagonal_vertices[kk+1] = v1->getPrev();
          }
          }
        }                                  
}/*end if (root1 not equal to root 2)*/
}
 
  /*second pass,  now all diagoals should belong to the same polygon*/
//printf("second pass: \n");
 
//  for(i=0; i<num_diagonals; i++)
//    printf("%i ", removedDiagonals[i]);
 
 
  for(i=0,k=0; i<num_diagonals; i++, k += 2)
    if(removedDiagonals[i] == 0) 
      {
 
 
    directedLine* v1=diagonal_vertices[k];
    directedLine* v2=diagonal_vertices[k+1];
 
 
 
    directedLine* ret_p1;
    directedLine* ret_p2;
 
    /*we ahve to determine whether v1 and v2 belong to the same polygon before
     *their structure are modified by connectDiagonal().
     */
    directedLine *root1 = v1->findRoot();
/*
    directedLine *root2 = v2->findRoot();
 
 
 
    assert(root1);      
    assert(root2);      
    assert(root1 == root2);
  */    
    sampledLine* generatedLine;
 
 
 
    v1->connectDiagonal(v1,v2, &ret_p1, &ret_p2, &generatedLine, ret_polygons);
    newSampledLines = generatedLine->insert(newSampledLines);
 
    ret_polygons = ret_polygons->cutoffPolygon(root1);
 
    ret_polygons = ret_p1->insertPolygon(ret_polygons);
 
    ret_polygons = ret_p2->insertPolygon(ret_polygons);
 
 
 
    for(Int j=i+1; j<num_diagonals; j++) 
      {
        if(removedDiagonals[j] ==0)
          {
 
        directedLine* temp1=diagonal_vertices[2*j];
        directedLine* temp2=diagonal_vertices[2*j+1];
               if(temp1==v1 || temp1==v2 || temp2==v1 || temp2==v2)
        if(! temp1->samePolygon(temp1, temp2))
          {
            /*if temp1 and temp2 are in different polygons, 
             *then one of them must be v1 or v2.
             */
 
 
 
            assert(temp1==v1 || temp1 == v2 || temp2==v1 || temp2 ==v2);
            if(temp1==v1) 
              {
            diagonal_vertices[2*j] = v2->getPrev();
              }
            if(temp2==v1)
              {
            diagonal_vertices[2*j+1] = v2->getPrev();
              }
            if(temp1==v2)
              {
            diagonal_vertices[2*j] = v1->getPrev();           
              }
            if(temp2==v2)
              {
            diagonal_vertices[2*j+1] = v1->getPrev();
              }
          }
          }
      }      
 
      }
 
 
  //clean up
  loopList->deleteLoopList();
  free(array);
  free(ranges);
  free(diagonal_vertices);
  free(removedDiagonals);
 
  *retSampledLines = newSampledLines;
  return ret_polygons;
}

Referenced by Subdivider::drawSurfaces().

MC_sweepY()

Int MC_sweepY	(	Int	nVertices,
		monoChain **	sortedVertices,
		sweepRange **	ret_ranges
	)

Definition at line 451 of file monoChain.cc.

{
  Int i;
  Real keyY;
  Int errOccur=0;
//printf("enter MC_sweepY\n");
//printf("nVertices=%i\n", nVertices);
  /*for each vertex in the sorted list, update the binary search tree.
   *and store the range information for each vertex.
   */
  treeNode* searchTree = NULL;
//printf("nVertices=%i\n", nVertices);
  for(i=0; i<nVertices; i++)
    {
      monoChain* vert = sortedVertices[i];
      keyY = vert->getHead()->head()[1]; //the sweep line
      directedLine *dline = vert->getHead();
      directedLine *dlinePrev = dline->getPrev();
      if(isBelow(dline, dline) && isBelow(dline, dlinePrev))
    {
//printf("case 1\n");
      //this<v and prev < v
      //delete both edges
      vert->isKey = 1;
      vert->keyY = keyY;
      treeNode* thisNode = TreeNodeFind(searchTree, vert, (Int (*) (void *, void *))compChains);
      vert->isKey = 0;
 
      vert->getPrev()->isKey = 1;
      vert->getPrev()->keyY = keyY;
      treeNode* prevNode = TreeNodeFind(searchTree, vert->getPrev(), (Int (*) (void *, void *))compChains);
      vert->getPrev()->isKey = 0;
 
      if(cuspType(dline) == 1)//interior cusp
        {
 
          treeNode* leftEdge = TreeNodePredecessor(prevNode);
          treeNode* rightEdge = TreeNodeSuccessor(thisNode);
          if(leftEdge == NULL ||  rightEdge == NULL)
        {
          errOccur = 1;
          goto JUMP_HERE;
        }
 
          directedLine* leftEdgeDline = ((monoChain* ) leftEdge->key)->find(keyY);
 
 
 
          directedLine* rightEdgeDline = ((monoChain* ) rightEdge->key)->find(keyY);
 
          ret_ranges[i] = sweepRangeMake(leftEdgeDline, 1, rightEdgeDline, 1);
        }
      else /*exterior cusp*/
        {
          ret_ranges[i] = sweepRangeMake( dline, 1, dlinePrev, 1);
        }
 
      searchTree = TreeNodeDeleteSingleNode(searchTree, thisNode);
      searchTree = TreeNodeDeleteSingleNode(searchTree, prevNode);
 
    }
      else if(isAbove(dline, dline) && isAbove(dline, dlinePrev))
    {
//printf("case 2\n");
      //insert both edges
      treeNode* thisNode = TreeNodeMake(vert);
      treeNode* prevNode = TreeNodeMake(vert->getPrev());
      
      vert->isKey = 1;
          vert->keyY = keyY;
      searchTree = TreeNodeInsert(searchTree, thisNode, (Int (*) (void *, void *))compChains);
          vert->isKey = 0;
 
          vert->getPrev()->isKey = 1;
          vert->getPrev()->keyY = keyY;
      searchTree = TreeNodeInsert(searchTree, prevNode, (Int (*) (void *, void *))compChains);
          vert->getPrev()->isKey = 0;
 
      if(cuspType(dline) == 1) //interior cusp
        {
//printf("cuspType is 1\n");
          treeNode* leftEdge = TreeNodePredecessor(thisNode);
          treeNode* rightEdge = TreeNodeSuccessor(prevNode);
              if(leftEdge == NULL || rightEdge == NULL)
        {
          errOccur = 1;
          goto JUMP_HERE;
        }
//printf("leftEdge is %i, rightEdge is %i\n", leftEdge, rightEdge);
          directedLine* leftEdgeDline = ((monoChain*) leftEdge->key)->find(keyY);
          directedLine* rightEdgeDline = ((monoChain*) rightEdge->key)->find(keyY);
          ret_ranges[i] = sweepRangeMake( leftEdgeDline, 1, rightEdgeDline, 1);
        }
      else //exterior cusp
        {
//printf("cuspType is not 1\n");
          ret_ranges[i] = sweepRangeMake(dlinePrev, 1, dline, 1);
        }
    }
      else
    {     
//printf("%i,%i\n", isAbove(dline, dline), isAbove(dline, dlinePrev));
      errOccur = 1;
      goto JUMP_HERE;
      
      fprintf(stderr, "error in MC_sweepY\n");
      exit(1);
    }
    }
 
 JUMP_HERE:
  //finally clean up space: delete  the search tree
  TreeNodeDeleteWholeTree(searchTree);
  return errOccur;
}

Referenced by MC_partitionY().