Include dependency graph for normal.c:
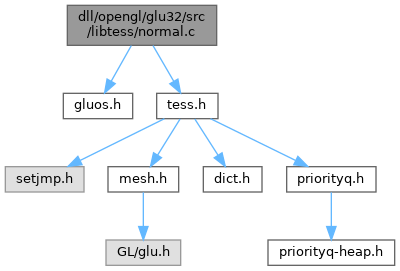
Go to the source code of this file.
Macros | |
| #define | TRUE 1 |
| #define | FALSE 0 |
| #define | Dot(u, v) (u[0]*v[0] + u[1]*v[1] + u[2]*v[2]) |
| #define | ABS(x) ((x) < 0 ? -(x) : (x)) |
| #define | S_UNIT_X 1.0 |
| #define | S_UNIT_Y 0.0 |
Functions | |
| static int | LongAxis (GLdouble v[3]) |
| static void | ComputeNormal (GLUtesselator *tess, GLdouble norm[3]) |
| static void | CheckOrientation (GLUtesselator *tess) |
| void | __gl_projectPolygon (GLUtesselator *tess) |
Macro Definition Documentation
◆ ABS
◆ Dot
◆ FALSE
◆ S_UNIT_X
◆ S_UNIT_Y
◆ TRUE
Function Documentation
◆ __gl_projectPolygon()
| void __gl_projectPolygon | ( | GLUtesselator * | tess | ) |
Definition at line 198 of file normal.c.
199{
202 GLdouble *sUnit, *tUnit;
204
210 computedNormal = TRUE;
211 }
212 sUnit = tess->sUnit;
213 tUnit = tess->tUnit;
215
216#if defined(FOR_TRITE_TEST_PROGRAM) || defined(TRUE_PROJECT)
217 /* Choose the initial sUnit vector to be approximately perpendicular
218 * to the normal.
219 */
221
222 sUnit[i] = 0;
225
226 /* Now make it exactly perpendicular */
231 Normalize( sUnit );
232
233 /* Choose tUnit so that (sUnit,tUnit,norm) form a right-handed frame */
237 Normalize( tUnit );
238#else
239 /* Project perpendicular to a coordinate axis -- better numerically */
240 sUnit[i] = 0;
243
244 tUnit[i] = 0;
247#endif
248
249 /* Project the vertices onto the sweep plane */
253 }
254 if( computedNormal ) {
255 CheckOrientation( tess );
256 }
257}
GLsizei GLenum const GLvoid GLsizei GLenum GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLint GLint GLint GLshort GLshort GLshort GLubyte GLubyte GLubyte GLuint GLuint GLuint GLushort GLushort GLushort GLbyte GLbyte GLbyte GLbyte GLdouble GLdouble GLdouble GLdouble GLfloat GLfloat GLfloat GLfloat GLint GLint GLint GLint GLshort GLshort GLshort GLshort GLubyte GLubyte GLubyte GLubyte GLuint GLuint GLuint GLuint GLushort GLushort GLushort GLushort GLboolean const GLdouble const GLfloat const GLint const GLshort const GLbyte const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLdouble const GLfloat const GLfloat const GLint const GLint const GLshort const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort const GLdouble const GLfloat const GLint const GLshort GLenum GLenum GLenum GLfloat GLenum GLint GLenum GLenum GLenum GLfloat GLenum GLenum GLint GLenum GLfloat GLenum GLint GLint GLushort GLenum GLenum GLfloat GLenum GLenum GLint GLfloat const GLubyte GLenum GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLint GLint GLsizei GLsizei GLint GLenum GLenum const GLvoid GLenum GLenum const GLfloat GLenum GLenum const GLint GLenum GLenum const GLdouble GLenum GLenum const GLfloat GLenum GLenum const GLint GLsizei GLuint GLfloat GLuint GLbitfield GLfloat GLint GLuint GLboolean GLenum GLfloat GLenum GLbitfield GLenum GLfloat GLfloat GLint GLint const GLfloat GLenum GLfloat GLfloat GLint GLint GLfloat GLfloat GLint GLint const GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat GLint GLfloat GLfloat const GLdouble const GLfloat const GLdouble const GLfloat GLint i
Definition: glfuncs.h:248
static void ComputeNormal(GLUtesselator *tess, GLdouble norm[3])
Definition: normal.c:76
Definition: mesh.h:114
Referenced by gluTessEndPolygon().
◆ CheckOrientation()
|
static |
Definition at line 141 of file normal.c.
142{
147
148 /* When we compute the normal automatically, we choose the orientation
149 * so that the sum of the signed areas of all contours is non-negative.
150 */
151 area = 0;
155 do {
159 }
161 /* Reverse the orientation by flipping all the t-coordinates */
164 }
168 }
169}
Definition: mesh.h:126
Definition: mesh.h:138
Referenced by __gl_projectPolygon().
◆ ComputeNormal()
|
static |
Definition at line 76 of file normal.c.
77{
80 GLdouble maxVal[3], minVal[3], d1[3], d2[3], tNorm[3];
81 GLUvertex *maxVert[3], *minVert[3];
84
85 maxVal[0] = maxVal[1] = maxVal[2] = -2 * GLU_TESS_MAX_COORD;
86 minVal[0] = minVal[1] = minVal[2] = 2 * GLU_TESS_MAX_COORD;
87
93 }
94 }
95
96 /* Find two vertices separated by at least 1/sqrt(3) of the maximum
97 * distance between any two vertices
98 */
99 i = 0;
103 /* All vertices are the same -- normal doesn't matter */
105 return;
106 }
107
108 /* Look for a third vertex which forms the triangle with maximum area
109 * (Length of normal == twice the triangle area)
110 */
111 maxLen2 = 0;
121 tNorm[0] = d1[1]*d2[2] - d1[2]*d2[1];
122 tNorm[1] = d1[2]*d2[0] - d1[0]*d2[2];
123 tNorm[2] = d1[0]*d2[1] - d1[1]*d2[0];
124 tLen2 = tNorm[0]*tNorm[0] + tNorm[1]*tNorm[1] + tNorm[2]*tNorm[2];
125 if( tLen2 > maxLen2 ) {
126 maxLen2 = tLen2;
127 norm[0] = tNorm[0];
128 norm[1] = tNorm[1];
129 norm[2] = tNorm[2];
130 }
131 }
132
133 if( maxLen2 <= 0 ) {
134 /* All points lie on a single line -- any decent normal will do */
137 }
138}
Referenced by __gl_projectPolygon().