sinhf.c File Reference

#include "libm.h"
#include "libm_util.h"
#include "libm_inlines.h"
#include "libm_errno.h"

Include dependency graph for sinhf.c:

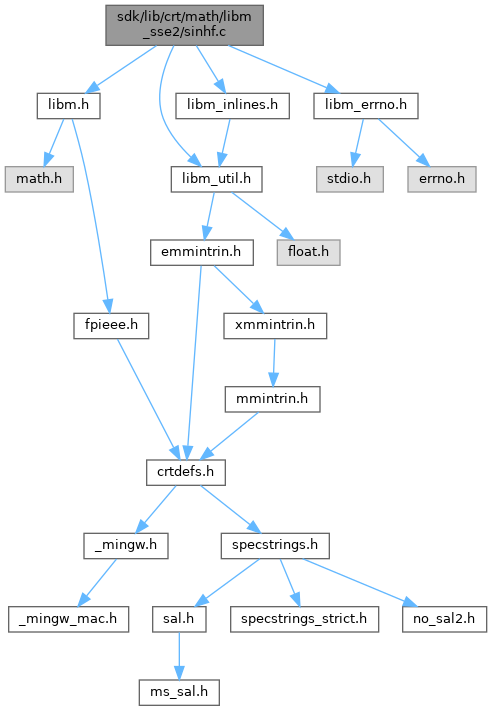
Go to the source code of this file.

Macros
#define	USE_SPLITEXP
#define	USE_SCALEDOUBLE_1
#define	USE_INFINITY_WITH_FLAGS
#define	USE_VALF_WITH_FLAGS
#define	USE_HANDLE_ERRORF

Functions
float	sinhf (float fx)

Macro Definition Documentation

USE_HANDLE_ERRORF

#define USE_HANDLE_ERRORF

Definition at line 34 of file sinhf.c.

USE_INFINITY_WITH_FLAGS

#define USE_INFINITY_WITH_FLAGS

Definition at line 32 of file sinhf.c.

USE_SCALEDOUBLE_1

#define USE_SCALEDOUBLE_1

Definition at line 31 of file sinhf.c.

USE_SPLITEXP

#define USE_SPLITEXP

Definition at line 30 of file sinhf.c.

USE_VALF_WITH_FLAGS

#define USE_VALF_WITH_FLAGS

Definition at line 33 of file sinhf.c.

Function Documentation

sinhf()

float sinhf

(

float

fx

)

Definition at line 51 of file sinhf.c.

{
  /*
    After dealing with special cases the computation is split into
    regions as follows:
 
    abs(x) >= max_sinh_arg:
    sinh(x) = sign(x)*Inf
 
    abs(x) >= small_threshold:
    sinh(x) = sign(x)*exp(abs(x))/2 computed using the
    splitexp and scaleDouble functions as for exp_amd().
 
    abs(x) < small_threshold:
    compute p = exp(y) - 1 and then z = 0.5*(p+(p/(p+1.0)))
    sinh(x) is then sign(x)*z.                             */
 
  static const double
    /* The max argument of sinhf, but stored as a double */
    max_sinh_arg = 8.94159862922329438106e+01, /* 0x40565a9f84f82e63 */
    thirtytwo_by_log2 = 4.61662413084468283841e+01, /* 0x40471547652b82fe */
    log2_by_32_lead = 2.16608493356034159660e-02, /* 0x3f962e42fe000000 */
    log2_by_32_tail = 5.68948749532545630390e-11, /* 0x3dcf473de6af278e */
    small_threshold = 8*BASEDIGITS_DP64*0.30102999566398119521373889;
  /* (8*BASEDIGITS_DP64*log10of2) ' exp(-x) insignificant c.f. exp(x) */
 
  /* Tabulated values of sinh(i) and cosh(i) for i = 0,...,36. */
 
  static const double sinh_lead[37] = {
    0.00000000000000000000e+00,  /* 0x0000000000000000 */
    1.17520119364380137839e+00,  /* 0x3ff2cd9fc44eb982 */
    3.62686040784701857476e+00,  /* 0x400d03cf63b6e19f */
    1.00178749274099008204e+01,  /* 0x40240926e70949ad */
    2.72899171971277496596e+01,  /* 0x403b4a3803703630 */
    7.42032105777887522891e+01,  /* 0x40528d0166f07374 */
    2.01713157370279219549e+02,  /* 0x406936d22f67c805 */
    5.48316123273246489589e+02,  /* 0x408122876ba380c9 */
    1.49047882578955000099e+03,  /* 0x409749ea514eca65 */
    4.05154190208278987484e+03,  /* 0x40afa7157430966f */
    1.10132328747033916443e+04,  /* 0x40c5829dced69991 */
    2.99370708492480553105e+04,  /* 0x40dd3c4488cb48d6 */
    8.13773957064298447222e+04,  /* 0x40f3de1654d043f0 */
    2.21206696003330085659e+05,  /* 0x410b00b5916a31a5 */
    6.01302142081972560845e+05,  /* 0x412259ac48bef7e3 */
    1.63450868623590236530e+06,  /* 0x4138f0ccafad27f6 */
    4.44305526025387924165e+06,  /* 0x4150f2ebd0a7ffe3 */
    1.20774763767876271158e+07,  /* 0x416709348c0ea4ed */
    3.28299845686652474105e+07,  /* 0x417f4f22091940bb */
    8.92411504815936237574e+07,  /* 0x419546d8f9ed26e1 */
    2.42582597704895108938e+08,  /* 0x41aceb088b68e803 */
    6.59407867241607308388e+08,  /* 0x41c3a6e1fd9eecfd */
    1.79245642306579566002e+09,  /* 0x41dab5adb9c435ff */
    4.87240172312445068359e+09,  /* 0x41f226af33b1fdc0 */
    1.32445610649217357635e+10,  /* 0x4208ab7fb5475fb7 */
    3.60024496686929321289e+10,  /* 0x4220c3d3920962c8 */
    9.78648047144193725586e+10,  /* 0x4236c932696a6b5c */
    2.66024120300899291992e+11,  /* 0x424ef822f7f6731c */
    7.23128532145737548828e+11,  /* 0x42650bba3796379a */
    1.96566714857202099609e+12,  /* 0x427c9aae4631c056 */
    5.34323729076223046875e+12,  /* 0x429370470aec28ec */
    1.45244248326237109375e+13,  /* 0x42aa6b765d8cdf6c */
    3.94814800913403437500e+13,  /* 0x42c1f43fcc4b662c */
    1.07321789892958031250e+14,  /* 0x42d866f34a725782 */
    2.91730871263727437500e+14,  /* 0x42f0953e2f3a1ef7 */
    7.93006726156715250000e+14,  /* 0x430689e221bc8d5a */
    2.15561577355759750000e+15}; /* 0x431ea215a1d20d76 */
 
  static const double cosh_lead[37] = {
    1.00000000000000000000e+00,  /* 0x3ff0000000000000 */
    1.54308063481524371241e+00,  /* 0x3ff8b07551d9f550 */
    3.76219569108363138810e+00,  /* 0x400e18fa0df2d9bc */
    1.00676619957777653269e+01,  /* 0x402422a497d6185e */
    2.73082328360164865444e+01,  /* 0x403b4ee858de3e80 */
    7.42099485247878334349e+01,  /* 0x40528d6fcbeff3a9 */
    2.01715636122455890700e+02,  /* 0x406936e67db9b919 */
    5.48317035155212010977e+02,  /* 0x4081228949ba3a8b */
    1.49047916125217807348e+03,  /* 0x409749eaa93f4e76 */
    4.05154202549259389343e+03,  /* 0x40afa715845d8894 */
    1.10132329201033226127e+04,  /* 0x40c5829dd053712d */
    2.99370708659497577173e+04,  /* 0x40dd3c4489115627 */
    8.13773957125740562333e+04,  /* 0x40f3de1654d6b543 */
    2.21206696005590405548e+05,  /* 0x410b00b5916b6105 */
    6.01302142082804115489e+05,  /* 0x412259ac48bf13ca */
    1.63450868623620807193e+06,  /* 0x4138f0ccafad2d17 */
    4.44305526025399193168e+06,  /* 0x4150f2ebd0a8005c */
    1.20774763767876680940e+07,  /* 0x416709348c0ea503 */
    3.28299845686652623117e+07,  /* 0x417f4f22091940bf */
    8.92411504815936237574e+07,  /* 0x419546d8f9ed26e1 */
    2.42582597704895138741e+08,  /* 0x41aceb088b68e804 */
    6.59407867241607308388e+08,  /* 0x41c3a6e1fd9eecfd */
    1.79245642306579566002e+09,  /* 0x41dab5adb9c435ff */
    4.87240172312445068359e+09,  /* 0x41f226af33b1fdc0 */
    1.32445610649217357635e+10,  /* 0x4208ab7fb5475fb7 */
    3.60024496686929321289e+10,  /* 0x4220c3d3920962c8 */
    9.78648047144193725586e+10,  /* 0x4236c932696a6b5c */
    2.66024120300899291992e+11,  /* 0x424ef822f7f6731c */
    7.23128532145737548828e+11,  /* 0x42650bba3796379a */
    1.96566714857202099609e+12,  /* 0x427c9aae4631c056 */
    5.34323729076223046875e+12,  /* 0x429370470aec28ec */
    1.45244248326237109375e+13,  /* 0x42aa6b765d8cdf6c */
    3.94814800913403437500e+13,  /* 0x42c1f43fcc4b662c */
    1.07321789892958031250e+14,  /* 0x42d866f34a725782 */
    2.91730871263727437500e+14,  /* 0x42f0953e2f3a1ef7 */
    7.93006726156715250000e+14,  /* 0x430689e221bc8d5a */
    2.15561577355759750000e+15}; /* 0x431ea215a1d20d76 */
 
  unsigned long long ux, aux, xneg;
  double x = fx, y, z, z1, z2;
  int m;
 
  /* Special cases */
 
  GET_BITS_DP64(x, ux);
  aux = ux & ~SIGNBIT_DP64;
  if (aux < 0x3f10000000000000) /* |x| small enough that sinh(x) = x */
    {
      if (aux == 0)
        /* with no inexact */
        return fx;
      else
        return valf_with_flags(fx, AMD_F_INEXACT);
    }
  else if (aux >= 0x7ff0000000000000) /* |x| is NaN or Inf */
    {
      if (aux > 0x7ff0000000000000)
        {
          /* x is NaN */
          unsigned int uhx;
          GET_BITS_SP32(fx, uhx);
          return _handle_errorf("sinhf", OP_SINH, uhx|0x00400000, _DOMAIN,
                               0, EDOM, fx, 0.0F, 1);
        }
      else
      return fx + fx;
    }
 
  xneg = (aux != ux);
 
  y = x;
  if (xneg) y = -x;
 
  if (y >= max_sinh_arg)
    {
      /* Return infinity with overflow flag. */
      if (xneg)
         return _handle_errorf("sinhf", OP_SINH, NINFBITPATT_SP32, _OVERFLOW,
                              AMD_F_OVERFLOW, ERANGE, fx, 0.0F, 1);
      else
         return _handle_errorf("sinhf", OP_SINH, PINFBITPATT_SP32, _OVERFLOW,
                              AMD_F_OVERFLOW, ERANGE, fx, 0.0F, 1);
    }
  else if (y >= small_threshold)
    {
      /* In this range y is large enough so that
         the negative exponential is negligible,
         so sinh(y) is approximated by sign(x)*exp(y)/2. The
         code below is an inlined version of that from
         exp() with two changes (it operates on
         y instead of x, and the division by 2 is
         done by reducing m by 1). */
 
      splitexp(y, 1.0, thirtytwo_by_log2, log2_by_32_lead,
               log2_by_32_tail, &m, &z1, &z2);
      m -= 1;
      /* scaleDouble_1 is always safe because the argument x was
         float, rather than double */
      z = scaleDouble_1((z1+z2),m);
    }
  else
    {
      /* In this range we find the integer part y0 of y
         and the increment dy = y - y0. We then compute
 
         z = sinh(y) = sinh(y0)cosh(dy) + cosh(y0)sinh(dy)
 
         where sinh(y0) and cosh(y0) are tabulated above. */
 
      int ind;
      double dy, dy2, sdy, cdy;
 
      ind = (int)y;
      dy = y - ind;
 
      dy2 = dy*dy;
 
      sdy = dy + dy*dy2*(0.166666666666666667013899e0 +
             (0.833333333333329931873097e-2 +
              (0.198412698413242405162014e-3 +
               (0.275573191913636406057211e-5 +
                (0.250521176994133472333666e-7 +
                 (0.160576793121939886190847e-9 +
                  0.7746188980094184251527126e-12*dy2)*dy2)*dy2)*dy2)*dy2)*dy2);
 
      cdy = 1 + dy2*(0.500000000000000005911074e0 +
             (0.416666666666660876512776e-1 +
              (0.138888888889814854814536e-2 +
               (0.248015872460622433115785e-4 +
            (0.275573350756016588011357e-6 +
             (0.208744349831471353536305e-8 +
              0.1163921388172173692062032e-10*dy2)*dy2)*dy2)*dy2)*dy2)*dy2);
 
      z = sinh_lead[ind]*cdy + cosh_lead[ind]*sdy;
    }
 
  if (xneg) z = - z;
  return (float)z;
}