tanf.c File Reference

#include "libm.h"
#include "libm_util.h"
#include "libm_inlines.h"
#include "libm_errno.h"

Include dependency graph for tanf.c:

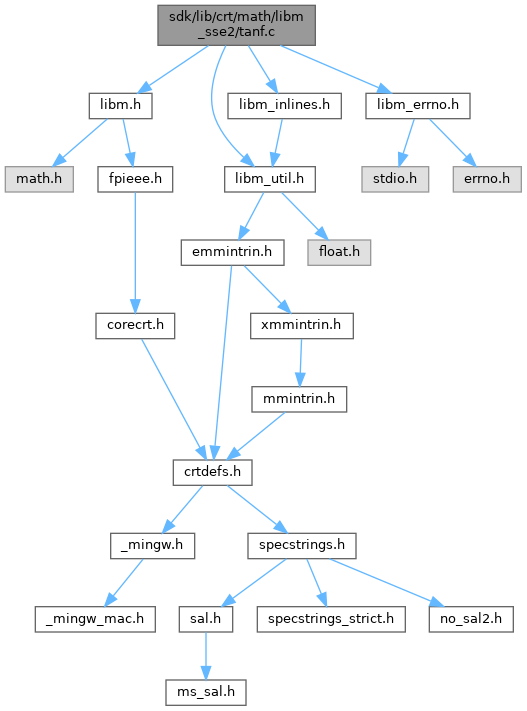
Go to the source code of this file.

Macros
#define	USE_REMAINDER_PIBY2F_INLINE
#define	USE_VALF_WITH_FLAGS
#define	USE_NANF_WITH_FLAGS
#define	USE_HANDLE_ERRORF

Functions
static double	tanf_piby4 (double x, int recip)
float	tanf (float x)

Macro Definition Documentation

USE_HANDLE_ERRORF

#define USE_HANDLE_ERRORF

Definition at line 33 of file tanf.c.

USE_NANF_WITH_FLAGS

#define USE_NANF_WITH_FLAGS

Definition at line 32 of file tanf.c.

USE_REMAINDER_PIBY2F_INLINE

#define USE_REMAINDER_PIBY2F_INLINE

Definition at line 30 of file tanf.c.

USE_VALF_WITH_FLAGS

#define USE_VALF_WITH_FLAGS

Definition at line 31 of file tanf.c.

Function Documentation

tanf()

float tanf

(

float

x

)

Definition at line 72 of file tanf.c.

{
  double r, dx;
  int region, xneg;
 
  unsigned long long ux, ax;
 
  dx = x;
 
  GET_BITS_DP64(dx, ux);
  ax = (ux & ~SIGNBIT_DP64);
 
  if (ax <= 0x3fe921fb54442d18) /* abs(x) <= pi/4 */
    {
      if (ax < 0x3f80000000000000) /* abs(x) < 2.0^(-7) */
        {
          if (ax < 0x3f20000000000000) /* abs(x) < 2.0^(-13) */
            {
              if (ax == 0x0000000000000000)
                return x;
              else
                return valf_with_flags(x, AMD_F_INEXACT);
            }
          else
            return (float)(dx + dx*dx*dx*0.333333333333333333);
        }
      else
        return (float)tanf_piby4(x, 0);
    }
  else if ((ux & EXPBITS_DP64) == EXPBITS_DP64)
    {
      /* x is either NaN or infinity */
      if (ux & MANTBITS_DP64)
        {
          /* x is NaN */
          unsigned int ufx;
          GET_BITS_SP32(x, ufx);
          return _handle_errorf("tanf", OP_TAN, ufx|0x00400000, _DOMAIN, 0,
                               EDOM, x, 0.0F, 1);
        }
      else
        {
          /* x is infinity. Return a NaN */
          return _handle_errorf("tanf", OP_TAN, INDEFBITPATT_SP32, _DOMAIN, AMD_F_INVALID,
                               EDOM, x, 0.0F, 1);
        }
    }
 
  xneg = (int)(ux >> 63);
 
  if (xneg)
    dx = -dx;
 
  if (dx < 5.0e5)
    {
      /* For these size arguments we can just carefully subtract the
         appropriate multiple of pi/2, using extra precision where
         dx is close to an exact multiple of pi/2 */
      static const double
        twobypi =  6.36619772367581382433e-01, /* 0x3fe45f306dc9c883 */
        piby2_1  =  1.57079632673412561417e+00, /* 0x3ff921fb54400000 */
        piby2_1tail =  6.07710050650619224932e-11, /* 0x3dd0b4611a626331 */
        piby2_2  =  6.07710050630396597660e-11, /* 0x3dd0b4611a600000 */
        piby2_2tail =  2.02226624879595063154e-21, /* 0x3ba3198a2e037073 */
        piby2_3  =  2.02226624871116645580e-21, /* 0x3ba3198a2e000000 */
        piby2_3tail =  8.47842766036889956997e-32; /* 0x397b839a252049c1 */
      double t, rhead, rtail;
      int npi2;
      unsigned long long uy, xexp, expdiff;
      xexp  = ax >> EXPSHIFTBITS_DP64;
      /* How many pi/2 is dx a multiple of? */
      if (ax <= 0x400f6a7a2955385e) /* 5pi/4 */
        {
          if (ax <= 0x4002d97c7f3321d2) /* 3pi/4 */
            npi2 = 1;
          else
            npi2 = 2;
        }
      else if (ax <= 0x401c463abeccb2bb) /* 9pi/4 */
        {
          if (ax <= 0x4015fdbbe9bba775) /* 7pi/4 */
            npi2 = 3;
          else
            npi2 = 4;
        }
      else
        npi2  = (int)(dx * twobypi + 0.5);
      /* Subtract the multiple from dx to get an extra-precision remainder */
      rhead  = dx - npi2 * piby2_1;
      rtail  = npi2 * piby2_1tail;
      GET_BITS_DP64(rhead, uy);
      expdiff = xexp - ((uy & EXPBITS_DP64) >> EXPSHIFTBITS_DP64);
      if (expdiff > 15)
        {
          /* The remainder is pretty small compared with dx, which
             implies that dx is a near multiple of pi/2
             (dx matches the multiple to at least 15 bits) */
          t  = rhead;
          rtail  = npi2 * piby2_2;
          rhead  = t - rtail;
          rtail  = npi2 * piby2_2tail - ((t - rhead) - rtail);
          if (expdiff > 48)
            {
              /* dx matches a pi/2 multiple to at least 48 bits */
              t  = rhead;
              rtail  = npi2 * piby2_3;
              rhead  = t - rtail;
              rtail  = npi2 * piby2_3tail - ((t - rhead) - rtail);
            }
        }
      r = rhead - rtail;
      region = npi2 & 3;
    }
  else
    {
      /* Reduce x into range [-pi/4,pi/4] */
      __remainder_piby2f_inline(ax, &r, &region);
    }
 
  if (xneg)
    return (float)-tanf_piby4(r, region & 1);
  else
    return (float)tanf_piby4(r, region & 1);
}

tanf_piby4()

static double tanf_piby4 ( double  x, int  recip  )

inlinestatic

Definition at line 51 of file tanf.c.

{
  double r, t;
 
  /* Core Remez [1,2] approximation to tan(x) on the
     interval [0,pi/4]. */
  r = x*x;
  t = x + x*r*
    (0.385296071263995406715129e0 -
     0.172032480471481694693109e-1 * r) /
    (0.115588821434688393452299e+1 +
     (-0.51396505478854532132342e0 +
      0.1844239256901656082986661e-1 * r) * r);
 
  if (recip)
    return -1.0 / t;
  else
    return t;
}

Referenced by tanf().