nsWeakReference Struct Reference
Collaboration diagram for nsWeakReference:
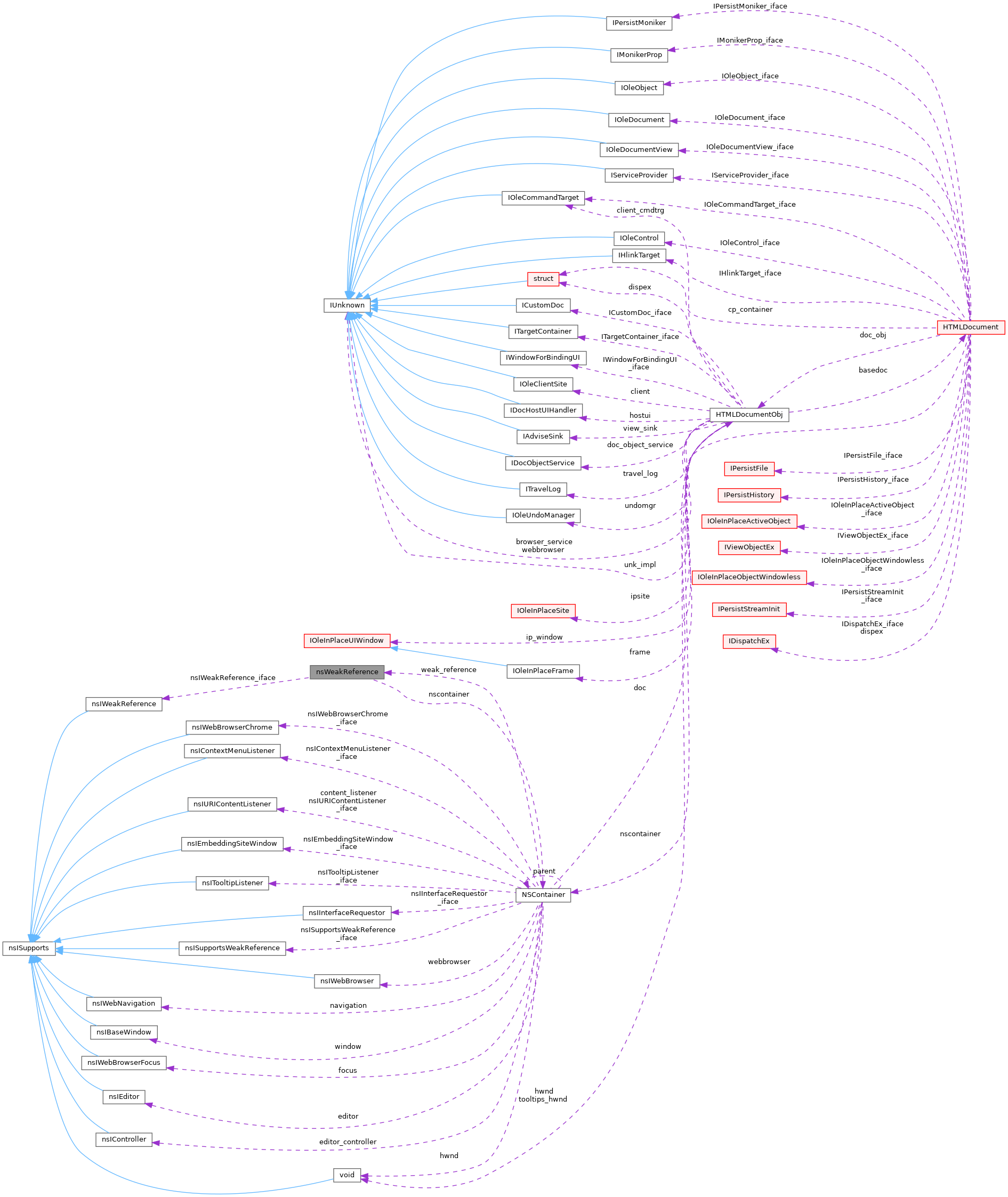
Public Attributes | |
| nsIWeakReference | nsIWeakReference_iface |
| LONG | ref |
| NSContainer * | nscontainer |
Detailed Description
Member Data Documentation
◆ nscontainer
| NSContainer* nsWeakReference::nscontainer |
◆ nsIWeakReference_iface
| nsIWeakReference nsWeakReference::nsIWeakReference_iface |
◆ ref
The documentation for this struct was generated from the following file:
- dll/win32/mshtml/nsembed.c